今回は線形回帰を取り上げてみたいと思います。
そもそも回帰(または回帰分析)というのは入力となる数値と出力となる数値の関係性を明らかにすることです。例えば、会社の社員数と売上の関係(社員がどのくらいいると、売上がどのくらいになるか)を回帰分析で求めることができれば、社員が100人いれば売り上げがおよそ○○円、社員が500人いれば売上がおよそ△△円といったように予測できるようになるということです。
非常に便利だと思いませんか?
今回はその回帰分析の中でも最も基本となる線形回帰を解説していこうと思います。
線形回帰の考え方を知ろう
まずは「線形」という言葉の意味から明確にしていきましょう。
線形とは1次式のことです。数式で表せば、例えば次のような形です。
$y=px+q$
中学の数学で習った一次関数の式ですね。$p$は$x$が変化した時に$y$がどのくらい変化するかを表し、$q$は$x$が$0$である時の$y$の値を表します。
つまり線形回帰とは、入力である$x$と出力である$y$の関係性を1次関数の数式を用いて表すことなのです。
ちなみに、上記の1次関数の式は直線を表すので、入力と出力の関係を直線で表すと表現することもできます。
それでは、具体例を見てみましょう。以下のグラフは50人の体重と身長のデータを表しています。
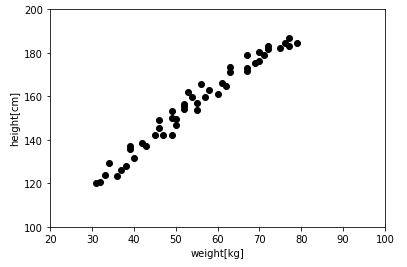
このデータから線形回帰で体重と身長の関係を求めてみましょう。今回は具体的な計算方法までは説明しませんので、結果だけを示したいと思います。
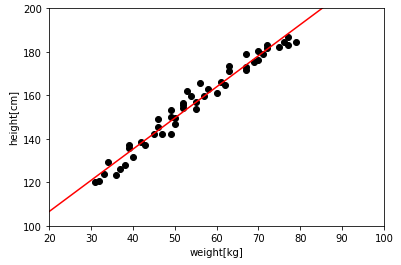
今回私が用いたデータでは、数式としては$y=1.43x+78$と求めることができました。グラフ中の赤い線がそれです。関係性が分かれば、任意の入力値(今回は体重)に対する出力値を予測することができます。例えば、グラフ上にデータがない$65kg$に対しても、数式に代入して$171cm$と予測することができます。
以上が線形回帰の基本的な考え方です。ここまで簡単のために入力に用いる数値は1つ(この例では体重)としてきましたが、実際は1つとは限りません。今回の例で言えば、体重に加えて、腹囲、体脂肪率など他の数値を併用してもよいのです。その場合数式は次のようになります。
$y=p_{1}x_{1}+p_{2}x_{2}+p_{3}x_{3}+……+q$
入力の数値が1種類である場合を単回帰、2つ以上ある場合を重回帰と言います。ただし、1次式を用いて入力と出力の関係性を表すという本質はいずれの場合も同じです。
最後に
今回は線形回帰の基本的な考え方について説明してみました。
初心者の方は線形回帰の細かい計算(1次式の求め方)はすぐに理解する必要はありませんが、原則的な考え方は理解しておくと今後必ず役に立ちますので、是非こちらの記事を使って学んでみてください!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!