今回は応用情報技術者試験でまず抑えておくべき2進数とn進数について解説していきます。
初心者の方でもこれを読めば、応用情報技術者試験に必要な知識を身につけられるようになっていますので、是非最後まで読んでみてください。
2進数やn進数とは?
まずは、2進数やn進数が一体なんであるのかを明記しておきましょう。
0 ~ n-1個までの数を用いて、あらゆる数値を表現する方法
n進数の一般的な定義はこの通りですが、抽象的で分かりづらいかもしれないので、早速具体例を見てみましょう。
まず私たちにとって最も馴染みがあるのは10進数です。nに10を当てはめればよいので、10進数は0~9を使って、あらゆる数値を表現する方法です。これはまさに私たちが普段の生活でやっていることですね。
しかし、コンピュータサイエンスなどの技術分野では10進数はほとんど使われず、最も基礎的で重要なのは、2進数です。
なぜ2進数が重要なのかは後述しますが、上記のn進数の定義に従うと、2進数は0と1であらゆる数値を表現する方法ということになります。
なぜ2進数が重要なのか?
2進数の中身を掘り下げていく前に、なぜ2進数が重要なのかを説明したいと思います。
10進数を使い慣れている我々の感覚からすると、2進数は使いづらいものです。様々な数を表現するのに0と1しか使えないというのは不便ですよね。
しかし、その直感的に分かりづらい2進数を使っているのにはちゃんとした理由があります。
コンピュータなどの電子機器はIC(Integrated Circuit=集積回路)と呼ばれる部品から構成されています。CPUやメモリなども中身はICの集合体です。

図をご覧になって分かるように、ICは黒いボディから銀色の足が何本も生えたような形をしています。そして、この銀色の足1本1本に加える電圧をON/OFFすることによってICは動作します。
ここで、電圧がOFFの状態を0、電圧がONの状態を1とすると、ICの状態を以下のように0と1を用いて表すことができるようになります。
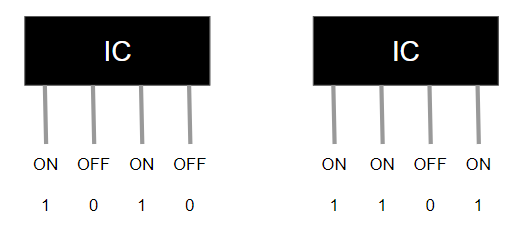
電圧はONとOFFの2つの状態しかないので、0と1の組み合わせによって、ICのあらゆる状態を表現可能です。これは、0と1によってあらゆる数を表現するという2進数の発想と全く同じです。
このような背景があるためデジタルの世界では2進数が基本になっています。
ちなみに、2進数は$1010$のように1または0が並びますが、1桁を1ビットとしてカウントします。$1010$であれば、数字が4つ並んでいるので4ビットということになります。
さらに、8ビットを1バイトとして定義します。よくデータ量の話をする時に使う○○バイトという単位はここからきています。
10進数を2進数(n進数)に変換する方法
2進数の重要性が分かったところで、まずは我々が普段使っている10進数を2進数で表現できるようになりましょう。
具体例として$157$という数字を取り上げてみます。これを2進数で表すことを考えるわけですが、その前に10進数の仕組みを復習しましょう。そもそも157という数字はどんな構造でしょうか?
$157~=~1×10^2~+~5×10^1~+~7×10^0$
ここから分かるように、10進数とは、10の累乗を基準として数値を表現しているとも言えます。$157$とは$10^2$の係数である$1$、$10^1$の係数である$5$、$10^0$の係数である$7$が並んでいると捉えることができます。
この考え方を応用すれば、$157$を2進数で表すためには、以下のような形を求めれいいはずです。
$157~=~P×2^p~+~Q×2^q~+~R×2^r~+~……~+S×2^0$ (A)
$PQR…S$とここで得られた係数を並べれば、2進数で表現したことになります。
では、具体的に(A)の形を求めていきましょう。
まず、$2^7=128$なので、$157=1×2^7~+…..$という形になることが分かります。次に、$157-128=29$なので、この残った$29$を2の累乗で表します。
そうすると、$2^4=16$であることから、$157~=~1×2^7~+~1×2^4~+…..$となることが分かります。同様に、$29-16=13$なので、この残った$13$を2の累乗で表します。
あとは同じです。$2^3=8$なので、$157~=~1×2^7~+~1×2^4~+~1×2^3…..$まで分かります。残るのは$13-8=5$ですが、これは$5=1×2^2~+~1×2^0$と暗算で分かりますね。
従って、157という数字を2の累乗で表すと、次のようになります。
$157~=~1×2^7~+~1×2^4~+~1×2^3~+~1×2^2~+~1×2^0$
2の累乗の抜けているところを補うと、以下のように表現できます。付け足したところは、係数が0なので、右辺の合計値に変更はありません。
$157~=~1×2^7~+~0×2^6~+~0×2^5~+~1×2^4~+~1×2^3~+~1×2^2~+~0×2^1~+~1×2^0$
この係数を並べればよいので、$157$を2進数で表した結果は$10011101$です。
2進数が特に重要なので、2進数で説明しましたが、一般的にn進数でも考え方は全く同じです。
例えば、8進数であれば、$157=2×8^2~+~3×8^1~+~5×8^0$なので、157を8進数で表すと$235$です。
2進数(n進数)を10進数に変換する方法
今度は、逆に2進数を10進数に変換する方法を考えてみます。
では、具体例として、$101101$という2進数が与えられたとします。これを10進数で表現してみます。
ただ、これは単純に前章で説明したことの逆をやるだけです。2進数が$101101$だということは、10進数とは以下のような関係が成立しているはずです。1つ前の10進数を2進数に変換する方法を思い出してください。
$1×2^5~+~0×2^4~+~1×2^3~+~1×2^2~+~0×2^1~+1×2^0~=~(10進数)$
ここまで分かれば、もう左辺を計算するだけで、答えは$45$です。
この考え方も2進数のみならず、一般的にn進数に当てはめることができます。
例えば、16進数で$125$という数値が与えられている時には、以下のような計算で10進数に変換することができます。
$1×16^2~+~2×16^1~+~5×16^0=293$
2進数で負の数を表現する方法
ここからは2進数で負の数をどう表すかを説明していきます。10進数のようにマイナスをつけるだけなら簡単ですが、2進数では考え方が異なるため、順を追って分かりやすく解説します。
まず、負の数とはどんなものかを10進数で考えてみましょう。例えば、$70$の負の数は$-70$で、$70+(-70)=0$のように足すと$0$になるという性質があります。
2進数もマイナスはありませんが、「足したら$0$になる」というのと近い発想を持って負の数を考えます。なので、「$1101$の負の数は?」と聞かれれば、$1101$に足して$0$になるような数が答えです。
$1101~+~?(負の数) =0$
ただ、イメージは$0$なのですが、2進数では$0$の考え方が若干異なるので、それを以下に示します。
$1101~+~?(負の数) =10000$ (右辺の最上位の桁は無視)
少し分かりづらいですが、足し算を行なった際に桁が1つ上がる(上記の例では4桁から5桁)るような数を負の数と考えます。ご覧の通り、最上位の桁を無視してしまえば$0$です。
求め方は後で説明しますが、答えだけ先に言ってしまうと、$1100$に対応する負の数は$0011$です。これから足し算を行なって、$1101$と$0011$の和が$10000$になることを確かめます。
ただ、ここまでで2進数の加算を説明していないので、少し寄り道になりますが、2進数の加算のルールを以下に記載します。
各桁に対して以下のルールで加算を行なう。
- $0~+~0=0$
- $1~+~0=1$
- $0~+~1=1$
- $1~+~1=10$(桁上がり)
このルールに沿って、$1101$と$0011$を足してみます。

右から順に各桁の加算を行ないます。一番右は$1+1$なので、桁上がりが発生します。そうすると、次の桁は$0+1$ではなく、$1+1$になり、再び桁上がりが発生します。これを繰り返していくと、上記のように結果が$10000$となります。
繰り返しになりますが、最上位の桁は無視するので、加算の結果が$0$となりました。従って、$1101$に対応する負の数は$0011$だと分かります。このような関係性を2の補数表現と言います。(1の補数表現もありますが、あまり使わないので、ここでは説明しません)
では、最後に2の補数表現を求める手順を紹介します。
①0と1を反転する。
例)1101⇒0010
②一番右の桁に1を加算
例)0010⇒0011
ちなみに、2の補数表現では、最上位の桁が符号を表しており、最上位が1の2進数と最上位が0の2進数は異符号になります。
2進数で小数を表現する方法
ここからは2進数で小数を表していきます。
ただ、実を言うと、基本の考え方はすでに説明済みです。例として、0.375という数値を2進数で表現してみましょう。
$(10進数)~=~P×2^p~+~Q×2^q~+~R×2^r~+~……~+S×2^0$ (A)
10進数を2進数に変換するときは、このような形に直すのが基本だと言いましたが、これは小数でも同じです。ただし、少数の場合は$2^0$で終わりではなく、$2^{-1}, 2^{-2}……$と続いていきます。
$0.375=1×2^{-2}~+~1×2^{-3}$
小数であっても(A)のように表現することができました。これでほとんど終わったも同然ですが、ここから2進数で表現していく方法が2通りあるので、それらを順を追って紹介します。
固定小数点表示
1バイトの2進数(8桁の2進数)で小数を表現することを考えます。
この時、固定小数点と呼ばれる方式では8桁のどこまでが整数(どこからが小数)であるかを予め決めておきます。
今回は、例えば5桁目までを整数と決めれば、0.375は1バイトの2進数で以下のように表されます。
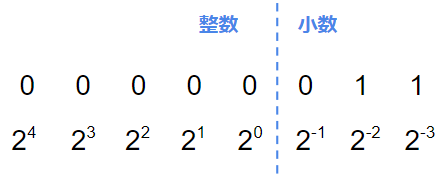
ちなみに、固定小数点表示では、最上位桁に符号の情報を持たせることもあります。その場合は以下のような形になります。

浮動小数点表示
不動小数点と呼ばれる方式では、$±p×2^{q}$という形で小数を表します。それぞれの数値に名前がついているので、以下にまとめておきます。

$0.375$(10進数)の例で考えると、以下のような表現の仕方が考えられます。
- $0.011~×~2^0$
- $0.11~×~2^{-1}$
これはどちらも同じ数値を表していますが、$11$の前についている$0$にはあまり意味がありません。無駄な情報を保持しておいても不必要にデータ量が増えてしまうだけなので、無駄を省くという観点から2つ目の表記方法が使われます。このように、仮数部の最上位桁を0以外にする操作を正規化と言います。
浮動小数点表示における一般的なデータの保持形式を紹介します。浮動小数点表示では、必要な情報を32ビットのデータ列で保持します。
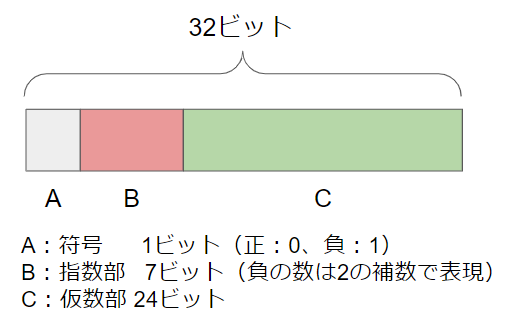
$0.375$の例で考えると、2進数表現は$0.11×2^{-1}$なので、A,B,Cに当てはまる数値は以下の通りです。少しだけ補足すると、指数部の$-1$は1(0000001)の補数で表現されています。
- A:0
- B:1111111
- C:11
ここまでで見て分かるように、固定小数点表示は分かりやすいですが、0がたくさん並んでしまうため、効率の面ではあまりよいとは言えません。一方、浮動小数点表示は直感的には少し分かりづらいところもありますが、無駄の無い効率的な表現となっているのが特徴です。
以上で、2進数とn進数の考え方と計算方法の説明を終わります!