今回はバンディットアルゴリズムを取り上げてみたいと思います。
活用と探索をバランスよく織り交ぜながら報酬の最大化を目指す強化学習のアルゴリズム
バンディットアルゴリズムは強化学習で用いられる手法なので、報酬の最大化は当然の目標なのですが、その過程で活用と探索をうまく使い分けるのがポイントです。
ここまで読んで、「そもそも活用と探索って何だろう?」と思った方もいると思うので、今回は活用と探索の意味から説明を始めて、バンディットアルゴリズムの具体例の紹介まで行ないたいと思います。
※強化学習の根本的な考え方を忘れてしまったという方は↓も併せてご覧ください。
バンディットアルゴリズムとは?
まずは例え話を通して活用と探索の考え方を理解していただきたいと思います。
あなたは新しい土地に引っ越してきたばかりで、これから買い物に行こうとしているとします。近所には以下の3件のスーパーがありますが、まだいずれも行ったことはありません。全く情報がないので、まずはスーパーAに行ってみることにしました。
実際に行ってみたらスーパーAは価格も品揃えもそこそこでした。次の機会に今度はスーパーBに行きました。そしたら、こちらは価格も安く、品揃えもよかったため、かなり満足できました。スーパーAに行くよりはスーパーBに行く方がよいことは分かりました。
ここで質問です。あなたは次回買い物に行く際には満足度の高いスーパーBに行きますか?それともより良い可能性を期待してスーパーCに行きますか?
前者を選んだ方はまさに活用をしたことになります。活用とは現在分かっている範囲で最も報酬が高い(=最善)の行動を選ぶことです。活用を繰り返していけば、安定的に高い報酬(今回の例えで言えば満足感)が得られます。ただし、未知の情報が残っている状況においては、より報酬の高い選択肢を捨てているという可能性もあります。もし、スーパーCがさらに満足度の高いスーパーであれば、スーパーBに行き続けることは損ですよね。
逆に後者を選んだ方は探索です。探索とは未知の情報を獲得しにいくことです。未知の情報を獲得するということは、得をすることもあれば損をすることもあります。スーパーCに行ってみて満足度が高ければ、「行ってよかった」となりますが、もし満足度が低ければ「スーパーBに行っておけばよかった」と後悔するでしょう。今回の例は選択肢が3つなので、まだよいですが、選択肢がたくさんある状況で何度も探索を行なって、失敗が続けば大損になりかねません。しかし、一方で大当たりを引く可能性もあるため、探索もとても重要なのです。
ここまでの説明で活用と探索の両方が大切であることが分かっていただけたかと思います。どちらか一方に偏り過ぎてしまっては最善の行動、つまり報酬の最大化を逃してしまうリスクがあります。
ここでバンディットアルゴリズムの登場です。冒頭にも述べたように、活用と探索をある一定のルールによってバランスよく織り交ぜたのがバンディットアルゴリズムなのです。
バンディットアルゴリズムの具体例
ここではバンディットアルゴリズムの具体例を2つ紹介していきます。
①ε-greedy方策
「イプシロングリーディー方策」と読みます。名前は難しそうですが、考え方はとてもシンプルです。ε-greedy方策ではある一定の確率で探索を行ないます。この確率の値のことを$ε$と言いますが、例えば$ε=0.1$であれば10%の確率で探索を実行するということです。つまり、10回中9回は現在知っている範囲のベストな行動を取って、1回だけ未知の行動にチャレンジしてみるということです。
Upper-Confidence Bound方策
略してUCBと呼ばれることもあります。UCBでは行動を選択する際に、得られる報酬の大きさとその行動を取った回数の少なさの両方が考慮されます。前者が活用の考え方、後者が探索の考え方に該当しますね。
では、もう少し詳細を具体例を交えて確認してみましょう。以下のようにくじがあり、1回引く毎に点数が書かれた玉が出てくるとします。何回もくじを引いて、得られる点数の合計をできるだけ大きくする方法をUCBで考えてみます。
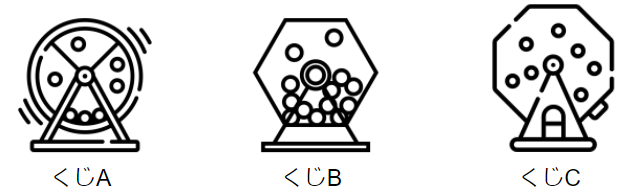
UCBの考え方では、次の式で定義される数値を全てのくじに対して毎回計算します。そしてこの数値が最も大きくなるくじを引いていきます。
$(くじXのこれまでの平均点数)+ \sqrt{\frac{2\log{(くじを引いた合計回数)}}{くじXを引いた回数}}$
Xに入るのはA、B、Cのいずれかです。
まず分かりやすいのは左の項の平均点数ですね。これは単純に平均なので、あるくじを10回引いたのであれば、点数の合計を求めて10で割るだけです。重要なことは上記の数式の値が大きいくじが選択されるということなので、平均点数が大きいものが選択されやすいということです。これはまさに過去の実績から最も点数が高そうなものを選ぶので活用ですね。
一方で、数式には平均点数以外の項もありますので、これも無視はできません。対数や平方根は忘れて、分母に着目しましょう。分母はあるくじが引かれた回数です。分母が小さい方が右の項は大きくなりますので、これまでに引かれた回数が少ない方が選択されやすいということです。これはまさにあまりよく分からないものにチャレンジするという探索ですね。
少し不正確な言い回しかもしれませんが、ここまでの話をイメージでまとめるのであれば、UCBは活用の度合いと探索の度合いの合計値が大きい選択肢を選ぶアルゴリズムです。つまり、どちらか一方だけが大きくても選ばれないので、必然的に活用と探索がバランスよく織り込まれていくのです。
最後に
今回はバンディットアルゴリズムの考え方を基礎の基礎から解説しました。
強化学習は教師あり学習や教師なし学習に比べて少し考え方が難しいですが、理解できると非常に面白いので、ぜひ理解できるまでこちらの記事を読み込んでいただければと思います!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!