今回はサポートベクターマシンを取り上げてみたいと思います。
様々なグループから成るデータの集合をもとに、グループ間の境界線を見つけることによって分類問題を解く手法
ディープラーニングが本格的に登場してくる以前は、機械学習の中でも頻繁に使われる手法の1つでした。
厳密に理解しようとすると数学の知識が必要になりますが、概要を掴むだけであればそれほど難易度は高くないので、分かりやすく解説していきたいと思います。
なお、サポートベクターマシーンはSVMと呼ばれることが多いので、以下ではSVMと表記していきます。
SVMは境界線を探す
SVMではデータのグループ間の境界線を探すことを目的とします。早速具体例を見ながら、その意味を確認してきましょう。
以下の図はある会社の社員の年齢と給与の関係を表しています。青い点が管理職、赤い点が非管理職であるとします。ただし、1つだけ黒色の点が存在します。この黒色の点は管理職、非管理職のどちらになるでしょうか?
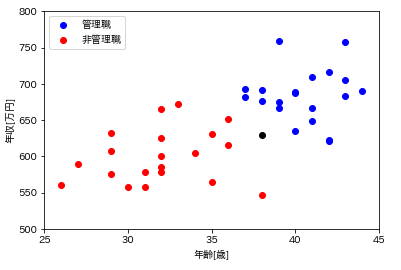
SVMで解くのであれば、まず管理職(青色)と非管理職(赤色)を分けるための境界線を探します。おそらく直感的には次のような境界線を引くことができると思います。
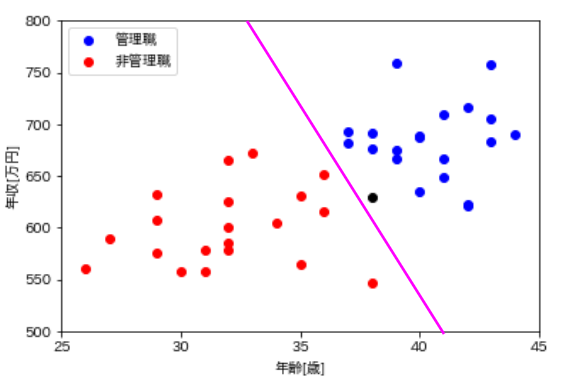
紫色の境界線の右側は全て管理職、左色は全て非管理職なので、うまくデータのグループの間に境界線を引くことができていますね。ここで、役職が未知である黒色の点に着目します。すると、黒色の点は境界線の右側にあることが分かりますね。境界線の右側にあるということは、この黒い点は「管理職である」という判定になります。
ここまでがSVMの基本的な考え方です。イメージを掴んでいただけたでしょうか?
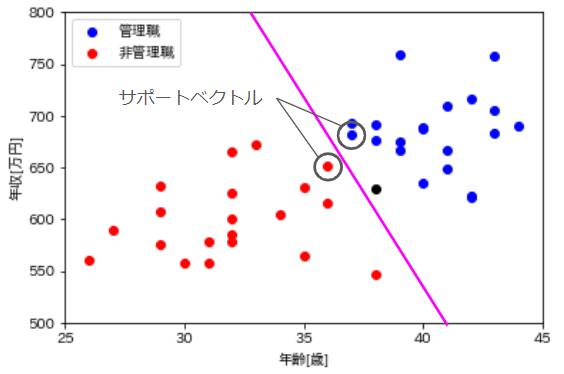
ちなみに、名前にも含まれているサポートベクトルというのは各々のグループで境界線に最も接近している点のことです。図中の紫の境界線に対しては、丸で囲んだ点がサポートベクトルです。数学的な詳細は割愛しますが、境界線を探す際にはこのサポートベクトルと境界線の間の距離ができるだけ大きくなることを条件としています。確かに、境界線とデータ点が離れている方がグループをくっきりと分けることができているということなので、直感的にも頷けますね。
ここまで2次元のデータ(変数が「年齢」と「年収」の2つ)を扱ってきましたが、SVMはさらに高次元のデータに対しても同様の考え方で適用できます。ただし、3次元の場合は立体なので、境界は「線」ではなく、「面」となります。それよりもさらに高次元になると、図のイメージを持つことは難しいですが、超平面と呼ばれます。
応用編:境界線が引けない時の対処法
SVMではグループ間の境界線を見つけ出すことが重要ですが、必ずしもうまく境界線が見つかるとは限りません。
例えば、以下のような分布のデータに対して境界線を引くことはできるでしょうか?
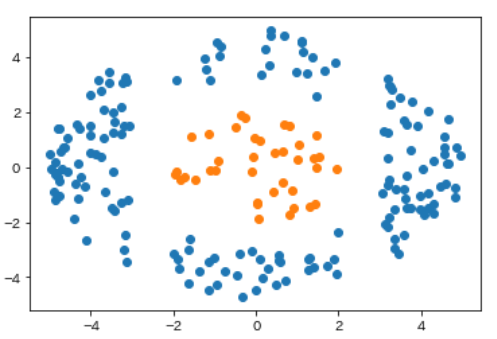
どのように直線を引いてみても、橙色と青色の点をくっきりと分けることは難しいと思います。
このような場合にはデータ点を敢えて高次元(この例では3次元以上)に写像することで境界を探します。写像というのはある点を別の点に移動させることです。例えば、先ほどの図を3次元にうまく写像することによって以下のような図に変換できます。
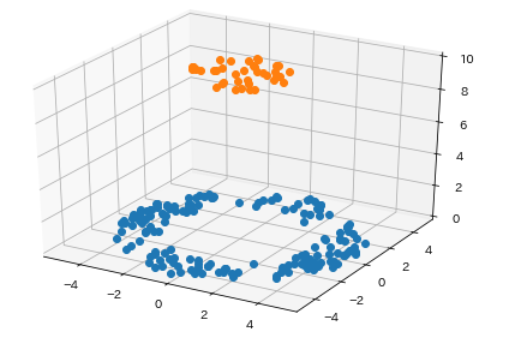
このような図であれば、橙色と青色の点の間に境界面が引けそうです。このように高次元に写像して境界を探す手法のことをカーネル法と言い、高次元に写像する関数のことをカーネル関数と言います。また、高次元に写像すると変数が増えるため、それに伴って一般的に計算量は増加します。数学的な詳細は割愛しますが、カーネル法では、その計算量を抑制するテクニックも知られており、それをカーネルトリックと呼びます。
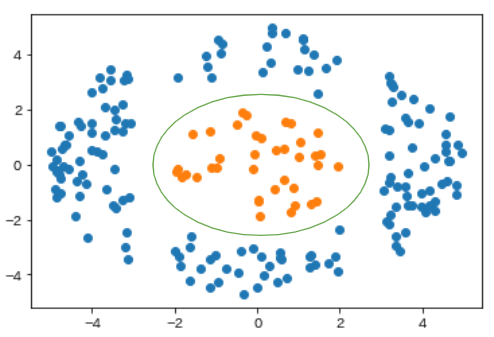
カーネル法を用いて高次元で境界を求めると、それを元の次元に戻した場合の境界は通常と少し異なります。2次元であればSVMの境界は直線になるのが一般的ですが、例えば上記の例であれば、境界は曲線となります。
最後に
今回はSVMの基本的な考え方について解説してみました。
サポートベクターマシンと名前は仰々しいですが、根本の考え方はシンプルであることがご理解いただけたかと思います!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!












