今回は有名な玩具であるハノイの塔を探索木を用いて攻略してみたいと思います。
※探索木の理解に不安がある方はまず↓をご覧ください。
探索木を用いて解けるということは、人工知能に解かせることができるということです。
図を使いながら丁寧に説明していきますので、探索木の応用編として是非学んでみてください。
ハノイの塔って何?
「ハノイの塔」という玩具をご存知ない方もいると思うので、まずはハノイの塔の遊び方を説明します。
ハノイの塔は以下のような玩具です。
家具の里(ベビーグッズ・おもちゃ)
3本のポールがあり、大小の異なる円盤がポールに刺さっています。この円盤をある一定のルールのもとでポールからポールへ移動させていき、移動が完了したらゲーム終了です。
さて、円盤の枚数が多いとゲームが非常に複雑になるので、今回用いるのは大中小の3種類の円盤とします。ポールは写真と同じように3本あるとします。
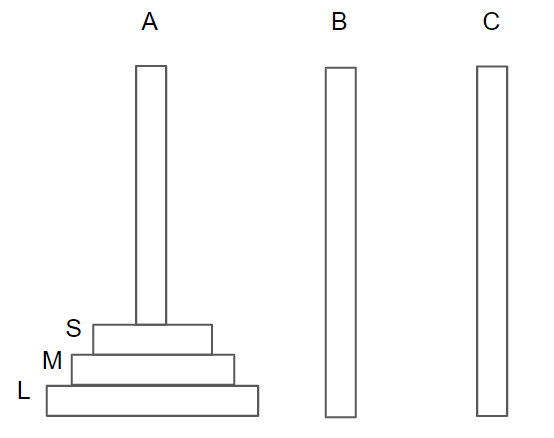
3本のポールを左から順にA,B,Cとし、円盤の小・中・大をそれぞれS,M,Lとします。今回のゲームではこの3枚の円盤を以下のようにAからCへ全て移動させたら完了とします。
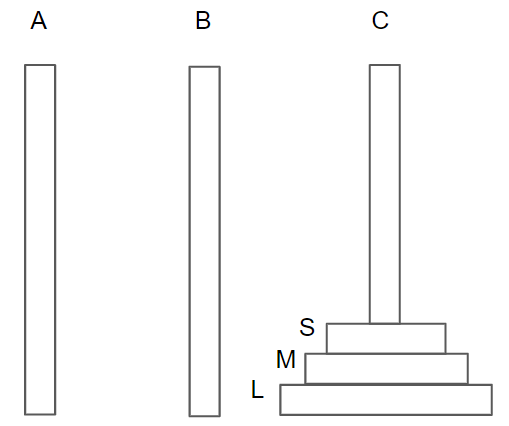
そして、円盤の移動や配置に際しては次の3つのルールがあります。
- 1回の動作で1枚の円盤を移動できる
- 円盤は上から順に移動する
- 大きい円盤を小さい円盤の上に置くことはできない
以上の条件を前提とし、探索木を用いてハノイの塔を攻略していきます。
探索木でハノイの塔を攻略
探索木を用いるために、状況をもう少し簡略化して表現します。

左図が初期状態で、S,M,Lの円盤全て図のような順序でがAのポールに刺さっていることを示します。一方で、右図は完了状態でS,M,Lの円盤全てが図のような順序でCのポールに刺さっていることを意味します。このような表記方法で探索木を作成していきます。
それでは、ここから順を追って考えていきます。まず初期はS,M,Lの全てがAにある状態ですから、円盤の移動規則に従うと、Sの円盤をBまたはCに移動させるしかありません。よって、探索木は次のようになります。
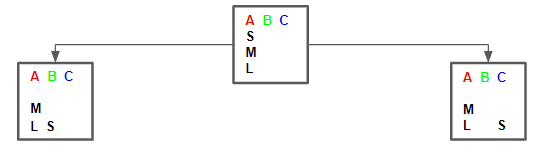
Sの円盤がAから移動したことにより、今度はMの円盤を移動できるようになりました。ただし、MがBとCのどちらに移動できるかは一手目のSの動きに依存します。なぜなら、MをSの上に置くことはできないからです。Mは必然的にSがいない方のポールへ動くことになります。
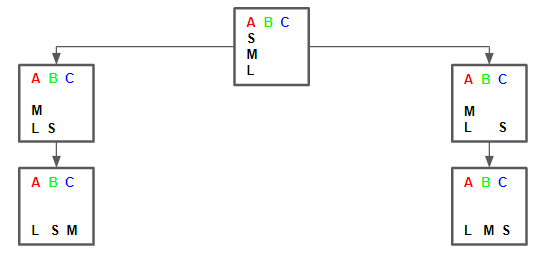
左側のパターンであれば、今度はSをAまはCに移すという行動が考えられます。また、右側のパターンであれば、SをAまたはBに移すという行動が考えられます。従って、探索木は次のようになります。
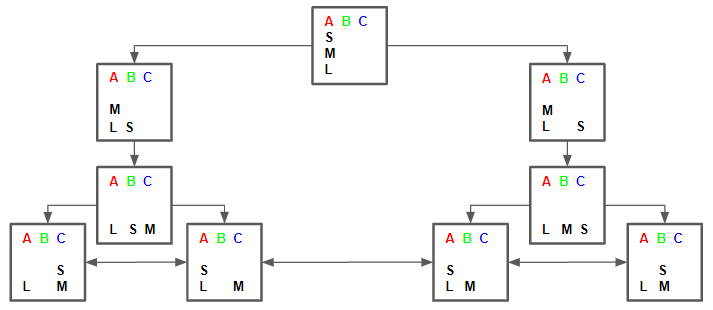
図の中心にある2つの状態は互いに1回の動作で移り変わりが可能なので、これらも互いに線で結んでおきます。
円盤の動かし方の要領が掴めてきたでしょうか?あとは同様の考え方で円盤を動かす作業をひたすら繰り返します。すると、最終的に探索木は以下のように完成します。
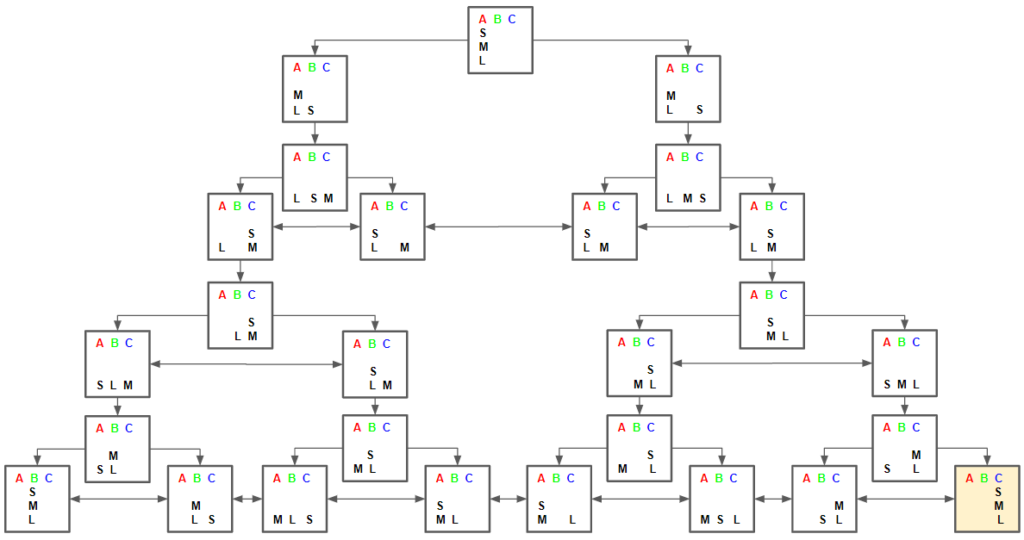
完成した探索木を見ると、一番右側のパターンに沿って行動すれば全ての円盤を最短でCに移すことができると分かります。
最後に
ハノイの塔、いかがだったでしょうか?
迷路に比べると探索木が複雑だったので、少し大変だと感じたかもしれませんね。
探索木を深く理解するためのいい練習になりますので、是非自分で手を動かして探索木を書いてみて下さい!!
最後になりますが、より詳しくAIを学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!