【わかりやすく解説】混同行列の概要をかみくだいて説明します

今回は混同行列を取り上げてみたいと思います。

混同行列

分類問題においてモデルの性能を評価するために用いる正方行列

機械学習はどのように問題を解かせるかというアルゴリズムも大切ですが、それによって出来上がったモデルを正しく評価することも同様に大切です。なぜなら、評価方法が不適切だと、それが本当によいモデルかどうかも分からず、必要な修正や改良を実行できないからです。

混同行列は特に二値分類で頻繁に用いられる評価方法なので、その中身と活用方法を基礎から解説していきます。

講師への質問OK! 16時間で学べるG検定対策講座【チートシート付き】

Table of Contents

混同行列とは？

分かりやすいように二値分類の具体例を使って見ていきましょう。今回は犬の画像判定、つまり画像が犬であるかそうでないかを判定するという問題を考えます。

このような問題では画像を機械学習のモデルに与えると、犬かどうかの判定が出力されるので、それが正しいかどうかを評価するわけですが、起こりえる結果は次の4つに集約されます。

モデルが犬だと判定して、実際に犬だった
モデルは犬だと判定したが、実際は犬ではなかった
モデルは犬ではないと判定したが、実際は犬だった
モデルは犬ではないと判定して、実際に犬ではなかった

さらにこれを表に焼き直すと、①～④は次のように表現することができます。

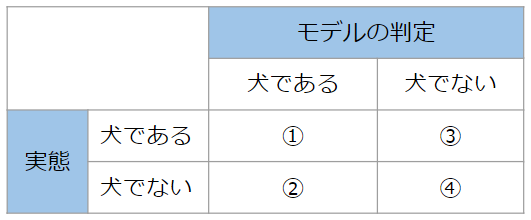
今回は仮に100枚の画像をモデルに判定させて、答え合わせをしたとしましょう。そうすると、100個の結果は①～④のいずれかの結果に当てはまるので、表の①～④に個数を書き込むことが可能ですね。例えば、次のようになります。

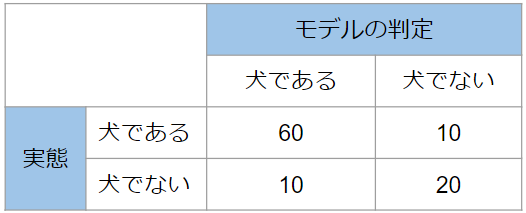
これがまさに混同行列です。結果を全て書き込んでいるので、数値を足し合わせると100になることに着目してください。混同行列を用いると、このように全ての結果を一望できるので、評価をするのにとても便利なのです。

混同行列の本質は以上なのですが、具体例を離れて一般的な表現に書き換えたいと思います。

まず「犬である」を陽性（Positive）とし、「犬でない」を陰性（Negative）とします。二値分類なので、本質的にはそれが分かるような表現（例えば0/1やA/Bなど）なら何でもよいのですが、一般的には陽性・陰性（Positive/Negative）がよく使われています。

そして、それに伴って表の①～④には以下のような名前が付与されています。モデルの予想と実態が一致しているものには真（True）、一致しなかったものには偽（False）がつきます。ただ、これもそのように呼ばれているというだけで、特に本質的なものではありません。

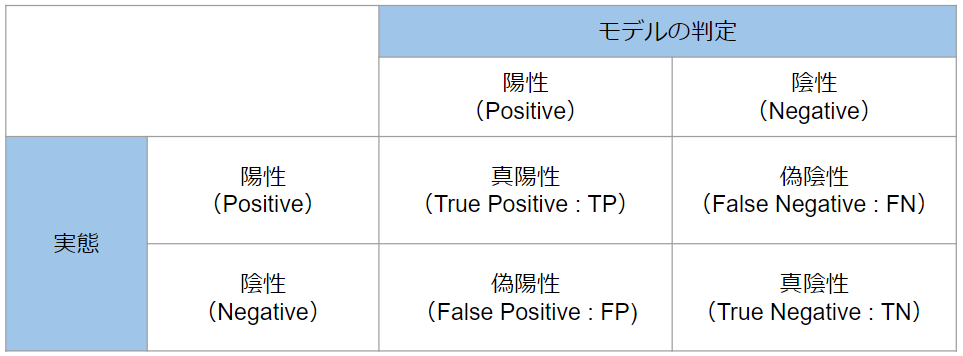
ここまで二値分類問題を前提に話を進めてきましたが、混同行列は二値より多い分類問題で使うことも可能です。二値分類の場合は表が$2\times 2$でしたが、N個の分類であれば表が$N\times N$になります。

混同行列の活用方法

ここからは混同行列を活用して得られる評価指標を紹介していきます。混同行列では結果を一望できますが、これから紹介する指標は、モデルの性能をズバリ数値で示すものです。

正解率

正解率は次の数式で定義されています。

$正解率 = \frac{TP+TN}{TP+FP+FN+TN}\times 100$

要するに全数の中でどのくらいモデルの予測と実態が一致していたかという割合です。これは非常に直感的で分かりやすいですね。先ほどの犬の画像判定の例では、100個の中で正しく判定できたのは$60+20=80$個なので、正解率は80%になります。

一見すると、この指標があれば十分なようにも思えますが、実はこの指標だと正しくモデルの性能を評価できないケースがあります。

例えば、工場で生産される部品の不良を機械学習で判定するというタスクがあるとします。一般的に工場で不良品が生産されてしまうことは稀なので、不良品の実態は1000個中2個だったとします。

ここで全ての部品を無条件に良品だと判定するようなモデルを用意します。全ての部品を良品だと判定してしまうわけですから、ほとんど何もしていないのに等しく、低品質なモデルです。

では、1000個の部品をこのモデルに判定させた時の正解率はいくつになるでしょうか？答えは99.8%という非常に高い数値をたたき出します。なぜなら、1000個中998個は良品なので、何も考えずに良品だと判定していれば998個は正解になるからです。これでは、正解率が高くてもよいモデルであるとは言えませんね。

このように場合によっては正解率が適切な評価指標にならないこともあるので、これから紹介するような他の指標もあります。

再現率

再現率は次の数式で定義されています。

$再現率=\frac{TP}{TP+FN}\times 100$

これは実態が陽性であるものの中でモデルが陽性だと判定した割合を表します。正解率に比べると少し難しいですね。先ほどの犬の画像判定の例をもう一度見ながら考えてみましょう。

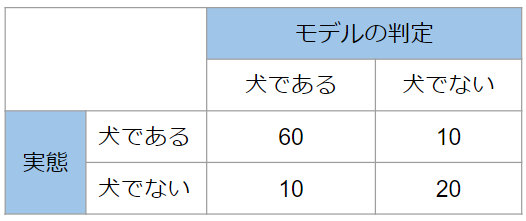
まず実態が犬である画像は$60+10=70$枚です。その中で、モデルが犬だと判定できたものは60枚です。従って、再現率は$\frac{60}{70}\times 100=$85%です。

この再現率を用いると、先ほどの不良品を判定する例の問題点が解決します。実態が不良品であったものが2個、モデルが不良品だと判定したものは0個なので、再現率は0%です。この数値を見れば、モデルに欠陥があることは一目瞭然になりますね。

ちなみに、再現率0%を改善するためには、部品を積極的に不良品だと判定するようにモデルを作り込んでいけばよいことになります。そうすると、不良品を絶対に見逃すことはなくなり、不良品が世の中に出ることを防げます。しかし、その反作用として、良品をうっかり不良品だと判定して廃棄することになるという可能性もあります。実際の場面では、何を重視するのかによって見るべき指標を変えていきます。「絶対に不良品を出したくない。そのためには良品を多少廃棄してしまうのは仕方ない」という立場に立つのであれば、再現率を評価指標として、それを高める工夫をしていくことになります。

適合率

適合率は次の式で定義されます。

$適合率=\frac{TP}{TP+FP}\times 100$

適合率はモデルが陽性だと判定したものの中で実態が陽性だったもの割合です。これも少し分かりづらいので、犬の画像判定の数字を使って具体的に計算をしてみましょう。上の表ではモデルが犬だと判定したものは70枚で、そのうち本当に犬だったのは60枚です。従って、適合率は $\frac{60}{70}\times 100=$85%と計算できます。

適合率が高いということは確実に陽性の判定ができているということです。言い換えると、陰性のものを誤って陽性だと判定することが少ないということです。

先ほどの部品の例で言えば、「良品をうっかり不良品と判定して廃棄するのはもったいない。そのために多少不良品を見逃すのは仕方ない」と考えるのであれば、適合率を評価指標として、それを高めるようにしていきます。

これは不良品の判定に対して消極的になるということでもあるので、適合率は上がる一方で、再現率は下がるということを知っておく必要があります。

F値

F値は次の数式で定義されています。

$F値 = \frac{2}{\frac{1}{適合率} + \frac{1}{再現率}}$

これは適合率と再現率の平均値（数学的には調和平均と言う）です。

ここまでで説明したように、再現率と適合率のどちらを重視するのかはスタンスによって異なります。そして、一方を高めようとすると、もう一方は低くなってしまいます。明確にスタンスが定まっていればよいですが、必ずしもそうとは限らないので、そのような場合には両者の平均値であるF値を指標としてバランスを保てるようにします。