今回は過学習と正則化を取り上げてみたいと思います。
- 過学習・・・モデルが訓練データに過度に適合して、汎用的な性能が低下すること
- 正則化・・・過学習を防ぐためにモデルのパラメータに制約を設けること
過学習は機械学習を活用する際には常に意識しなければならない問題です。過学習を起こしてしまうと、学習時にはよさそうに見えても、いざ本番で使おうと思ったら使えないということにもなりかねません。
今回は過学習が発生してしまう背景を説明したうえで、その対処法である正則化にも言及していきたいと思います。
過学習とは?
機械学習のそもそもの目的は学習したモデルを様々なデータに適用して、分類や回帰といった種々の問題を解くことです。
「様々なデータに適用して」ということは高い汎用性が期待されますが、実際に訓練に使用できる手元のデータは有限です。例えば、「猫の画像分類をしたい」と思って、機械学習のモデルを訓練するとしても、世界中のありとあらゆるタイプの猫の画像を用意して学習させるというの実質的に不可能です。実際に使えるのは、手持ちの限られた猫の画像だけです。
つまり、機械学習においては有限な量のデータを訓練に使って、いかに高い汎用性を持たせるかという点が常に大きな課題となります。
ここで考えられる最悪のケースは、訓練に使用したデータに対しては高い性能を示すが、それ以外のデータに対しては性能が低下するということです。訓練時には高い性能を発揮するので、一見よいモデルができたかのように見えますが、訓練に使ったことのないデータを与えると性能を発揮しなくなるので、実践では使えません。人間に例えて言うなら、テスト前に対象範囲の問題集を意味も解らず丸暗記してテストに臨むようなものです。丸暗記なので問題集の問題がそのまま出れば解けますが、少し捻りを加えたらお手上げになります。
ここで説明したことがまさに過学習です。もう少し一般化していうと、訓練データに過剰な適合をして汎化性能が低下してしまうことです。
過学習の要因は様々ありますが、1つ簡単な具体例を挙げてみたいと思います。先ほどの猫の画像分類の訓練で、仮に黒猫の画像ばかりを使ってしまったとします。そうすると、モデルは黒猫に対する識別能力を訓練によって磨いていきますが、黒以外の猫については全く未知です。実際には様々な色の猫がいるわけですから、このモデルを汎用的な分類に用いてしまうと、当然ながら高い精度を出すことはできません。
ここまでで、過学習が大きな問題であることは分かっていただけたと思うので、ここからはその対策である正則化を説明したいと思います。
過学習を防ぐための正則化
正則化の説明をするために、機械学習における訓練過程の説明から始めていきたいと思います。
モデルを訓練するとは、一言で言うと、モデルの出力と正解の差が小さくなるようにパラメータを調整することです。
パラメータというのは、モデルの性能を決める調整可能な数値のことで、例えばニューラルネットワークであれば、重みといったパラメータを持ちます。また、単回帰であれば$y=ax+b$という数式で近似をするので、$a,b$がパラメータです。
簡単な数式で書けば、パラメータの調整によって以下の$L$の値を小さくすることが学習の目的です。
$L =(正解 ー モデルの出力)^2$
学習のイメージを掴んでいただくために具体例を出しましょう。ここでは、以下のデータを説明するような回帰曲線を求めたいとします。
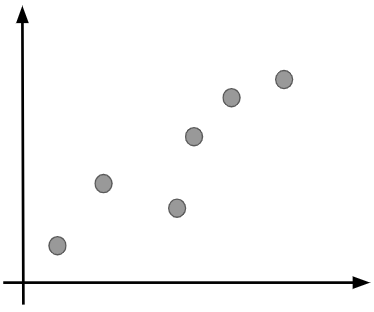
始めのうちは学習が進んでいないので、データとモデルの差は大きくなります。
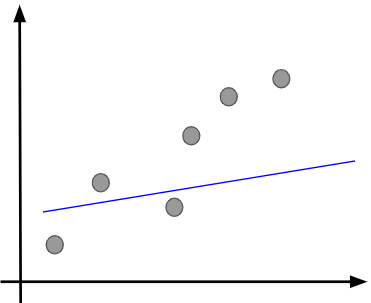
そして、徐々に学習が進んでパラメータが調整されてくると、データとモデルの差が縮まっていきます。
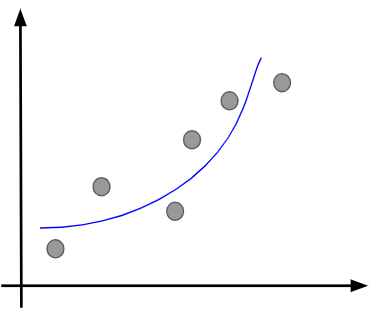
ただし、$L$の値を小さくすることが目的であるため、さらに学習を繰り返していけば、さらにモデルとデータの差を縮めようとするので、最終的には以下のようになるでしょう。
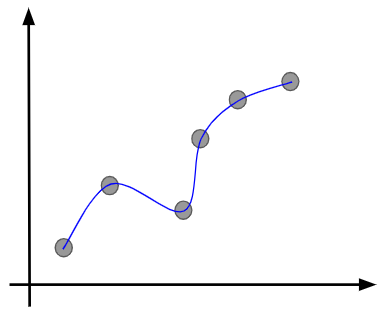
ただし、見て分かるように、この状態は明らかに訓練データに過剰に適合しており、過学習が疑われます。イメージ的には1つ上の図のような状態に落ち着くのが望ましいと言えるでしょう。このような状況になってしまったのは、データとモデルの出力の差を小さくすることだけを目的としたために、パラメータがそれを目指して調整されてしまったからです。
言い換えれば、そもそもの$L$の定義がデータ(正解)とモデルの出力の差だけになっていたことがよくなかったので、この$L$に正則化項と呼ばれるものを追加します。
$L =(正解 ー モデルの出力)^2 + 正則化項$
こうすると、ただ単に正解とモデルの出力の差を小さくするだけでは、$L$の値は小さくなりません。正則化項も含めて$L$の値を小さくしていくことが目的になります。数学的な詳細は省きますが、この正則化項にはパラメータが動ける範囲を制約する効果があります。パラメータが自由に動けるが故に訓練データに過剰適合できてしまうので、その自由を制約してしまえばよいという発想です。
ここまでが正則化の基本的な考え方です。正則化項の例としては次のようなものがあります。
| 正則化項 | 概要 |
|---|---|
| L1正則化(ラッソ回帰) | 重要度の低いパラメータを0にする効果がある |
| L2正則化(リッジ回帰) | パラメータを全体的に小さく保つ効果がある |
| Elastic Net | L1正則化とL2正則化を組み合わせた手法 |
最後に
今回は過学習と正則化について解説をしました。
最初にも述べたように、過学習は機械学習において常に考慮すべき重要な課題です。その対処法である正則化と併せて、本記事を通して基礎をしっかりと身につけていただければ幸いです!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!














