【考え方を理解しよう】強化学習の状態価値関数と行動価値関数を解説

今回は強化学習の基礎ともいえる状態価値関数と行動価値関数を取り上げてみたいと思います。

状態価値関数 $V_{\pi}(s)$

方策$\pi$のもとで、初期状態をsとした場合の累積報酬の期待値

行動価値関数 $Q_{\pi}(s,a)$

方策$\pi$のもとで、初期状態sにおいて行動aを取った場合の累積報酬の期待値

まずはそれぞれの定義を書いてみましたが、これだけでは抽象的でなかなか理解できませんね。

ここからはこれらを理解する前提となる知識を含めて順を追って説明をしていきたいと思います。

講師への質問OK! 16時間で学べるG検定対策講座【チートシート付き】

Table of Contents

累積報酬とは？

まずは状態価値関数と行動価値関数の定義に登場した累積報酬という言葉の中身から明らかにしていこうと思います。

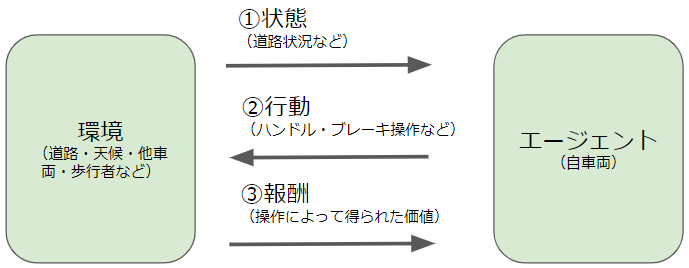
機械学習の大分類で説明したように、強化学習というのは以下に示すような設定で行なわれ、エージェントが行動した際に得られる報酬を大きくすることが目的でした。

用語	一般的な定義	自動運転の場合
エージェント	タスクの主要プレイヤー	自分の車
環境	タスクの土台となる条件	道路、天候、他車両、歩行者など
行動	エージェントの動作	ハンドルやブレーキの操作など
状態	環境がどのようであるかの情報	路面状態、車両の数・位置など
報酬	行動の結果によってもたらされる価値	無事故、目的地到達など

累積報酬というのは文字通り報酬を足しわせたものという意味なので、あるステップから最終ステップまでに得られるであろう報酬の合計値です。

tステップ目の状態、行動、報酬をそれぞれ$s_{t}, a_{t}, r_{t}$と表すとします。その場合の累積報酬$R_{t}$（t+1ステップ以降から最終ステップまでに得られるであろう報酬の合計）は次の式で記述することができます。

$R_{t} = r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\gamma^3 r_{t+4}+… \\= \sum_{k=1}^\infty \gamma^{k-1} r_{t+k}$

基本的には言葉通りに報酬の足し合わせを意味する数式になっているかと思います。ただし、皆さんもすでにお気づきのように各ステップの報酬に$\gamma$のべき乗が掛けられています。これは一体何を意味するのでしょうか？この$\gamma$は割引率と呼ばれ、0以上1未満のハイパーパラメータ（学習によって求めるのではなく、事前に人間が決めておく数値）です。累積報酬を考える際には直近に得られる報酬を重視するというのが基本スタンスです。なぜなら、ずっと先のステップのことはよく分からないため、いくら報酬が高そうであっても、本当に得られるかどうかが不明だからです。従って、将来の報酬の影響を小さくするために割引率$\gamma$が導入されました。先のステップになればなるほど$\gamma$の累乗の指数が大きくなるので、その報酬値が小さく見積もられることがご理解いただけるかと思います。

ここまでが累積報酬の説明です。強化学習ではとにかくこの累積報酬を大きくするように行動していくことが目的になります。

どうやって累積報酬を最大にするのか？

ここまでで累積報酬を最大にすればよいということは分かりましたが、累積報酬が最大になるような行動を取らせるためには何をすればよいでしょうか？

累積報酬は、数式をご覧いただくと、任意のt番目のステップに対して定義可能であることが分かると思います。つまり、あらゆるステップにおいて累積報酬を計算しておけば、それがtステップ目の状態$s_{t}$はどのくらい価値があるのかを表すことになります。何度も言っているように強化学習は累積報酬を大きくすることが目的ですから、累積報酬が大きい状態というのは価値が高く、累積報酬が小さい状態は価値が低いと解釈することができます。

このようにして各状態$s_{t}$の価値を表したものを状態価値関数と言います。考え方はご理解いただけたと思いますので、状態価値関数$V$を数式で表現してみましょう。

$V_{\pi}(s) = E_{\pi} [R_{t}|s_{t}=s]$

ここまで累積報酬がそのまま状態価値関数であるかのように記述しましたが、厳密に言うと、状態価値関数は累積報酬の期待値です。累積報酬は各ステップの報酬の単純な和ですが、各ステップの報酬と言うのは一意的に決まるものではありません。なぜなら、各ステップにおいて選択できる行動は基本的に複数あり、どの行動を選ぶかによって得られる報酬は異なるからです。言い換えれば、ある状態$s_{t}$において、「ハンドルを右に切れば報酬は10、ハンドルを左に切れば報酬は5」のようになっているということです。このような状況を扱うために、先ほども書いたように、報酬は期待値で計算されるというわけです。

さて、期待値を計算するには各行動を取った際に得られる報酬に加えて、各行動を取る確率も必要です。この確率を決めるのが方策です。方策は行動の指針や戦略のようなもので、例えば「○○な状況ではハンドルを右に切る」「△△な状況ではブレーキを踏む」といったものと考えればよいでしょう。方策が決まれば、各状態においてどんな行動をどのくらいの確率で選択するかが分かるので、報酬の期待値を計算することができます。

状態価値関数の定義式に$\pi$という文字が含まれていますが、これが方策を表す記号です。以下の例から分かるように、累積報酬の期待値は方策によって値が変わるので、状態価値関数は「ある方策$\pi$のもとでの累積報酬の期待値」ということになります。

状態$s_{t}$における行動	方策1での確率	方策2での確率	報酬
ハンドルを右に切る	0.5	0.2	10
ハンドルを左に切る	0.4	0.3	5
ブレーキをかける	0.1	0.5	15

方策1での報酬期待値：$0.5×10+0.4×5+0.1×15 = 8.5$
方策2での報酬期待値：$0.2×10+0.3×5+0.5×15 = 11$

繰り返しになりますが、ここまでで状態の価値を定義することができたので、累積報酬を大きくするには、価値が高い状態を見つけ出して辿っていけばよいということになります。すなわち、最適な状態価値関数を求めることが累積報酬を最大にすることにつながると言えます。
（状態関数の最適化については、また別の機会に記事にしてみようと思います）

行動価値関数とは?

最後に行動価値関数を導入します。
ただ、状態価値関数が理解できたのであれば、行動価値関数はそれほど難しいものではありません。

状態価値関数$V_{\pi}(s)$はある状態$s_{t}$の価値でした。それに対して、行動価値関数はある状態$s_{t}$においてある行動$a_{t}$を取った場合の価値を表します。

$Q_{\pi}(s,a) = E_{\pi}[R_{t}|s_{t}=s,a_{t}=a]$

数式の見た目で言っても、変数に行動$a_{t}$が含まれている点が状態価値関数とは異なります。先ほども言ったように、ある状態$s_{t}$においては、基本的に取り得る行動は複数あり、状態価値関数を計算する場合には、これらの行動すべてを考慮しなければなりません。一方で、行動価値関数の場合には「行動$a_{t}$を取った場合の」という前提が入るので、状態$s_{t}$で取り得る全ての行動を考慮する必要はなく、そのうちの1つの$a_{t}$だけを考慮すればよいということになります。これが状態価値関数と行動価値関数の違いです。

ここまでで見てお分かりいただけるように、状態価値関数と行動価値関数は「ある状態において全ての行動を考慮するのか、またはある1つの行動だけに着目するのか」といった違いだけで本質的に大きく変わるものではありません。これらの価値関数は、その最適化の手法に応じて使いやすいものを使っていくという使い分けになります。