今回はROC曲線とAUCを取り上げてみたいと思います。
- ROC曲線・・・陽性と見なす確率の閾値を変化させた際の真陽性率と偽陽性率の関係を表す曲線
- AUC・・・ROC曲線の下側の面積
ROC曲線やAUCは二値分類問題において機械学習のモデルを評価するために使用されます。混同行列からは正解率・再現率・適合率など様々な評価指標が得られることは以前説明しましたが、このROC曲線やAUCも混同行列から求めることができます。
とはいえ、上記の定義を見ただけではよく分からないという方が多いと思うので、基礎から順を追って解説していきます。
ROC曲線とは?
ROC曲線は二値分類問題が対象になるので、入力された画像が猫であるかどうかを判別するタスクを例に考えてみましょう。入力された画像が猫であれば陽性(Positive)、猫でなければ陰性(Negative)です。
二値分類問題ではロジスティック回帰が用いられるので、今回のケースであれば機械学習のモデルが出力するのは画像が猫である確率です。この出力に対して、例えば「確率が60%以上であれば猫の画像であると判断する」と言ったように判断の閾値を決めて、「猫である」「猫ではない」の結論を出します。
正しく学習できているモデルであれば、ある閾値を決めた時に、閾値以上は全て陽性、閾値未満は全て陰性となっているはずです。一方で、モデルが不正確であれば、閾値を決めてもうまく陽性と陰性が分離できず、閾値以上でも陰性が混在する、閾値未満でも陽性が混在するという問題が発生します。
まさにここを評価するのがROC曲線です。ROC曲線はある閾値を決めた時に陽性と陰性がどのくらい適切に分離されているかを表します。
では、ここから順にROC曲線の描き方を見ていきましょう。まず、猫の画像認識に対して以下のような結果があったとします。「猫」の文字が書かれた四角が実際の猫の画像で、各四角の下の数字は、モデルが予測した画像が猫である確率です。

ROC曲線は2次元のグラフなので、描画をする前にX軸とY軸を次のように定義します。
| 軸 | 名称 | 意味 |
|---|---|---|
| X | FPR | 全ての陽性の中で、モデルが陽性だと判定できた割合 |
| Y | TPR | 全ての陰性の中で、モデルが陽性だと判定してしまった割合 |
まずは仮に閾値を1.0にしてみましょう。つまり、確率が1.0以上であれば陽性(「猫」という判定)になりますが、確率が1.0以上の画像はありません。従って、FPR、TPRともに0なので、左下に点を打ちます。
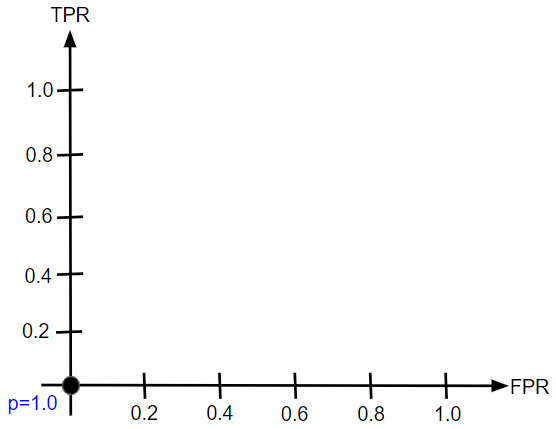
次は閾値を0.8にします。この場合は右側の2つが陽性判定です。3枚の猫の画像のうちで2枚を正しく猫だと判定できたので、TPR$=\frac{2}{3}$です。一方で、犬を誤って猫と判定しいるのは1つもないので、FPRは依然として0です。
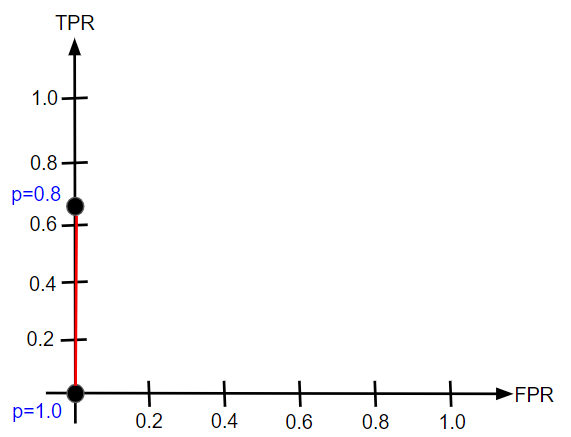
次は閾値を0.7にします。この時は犬を誤って猫と判定するケースが1つ発生します。犬の画像は全部で4件なので、FPR$=\frac{1}{4}$となります。陽性判定は閾値が0.8の時から変化がないため、TPRにも変化はありません。
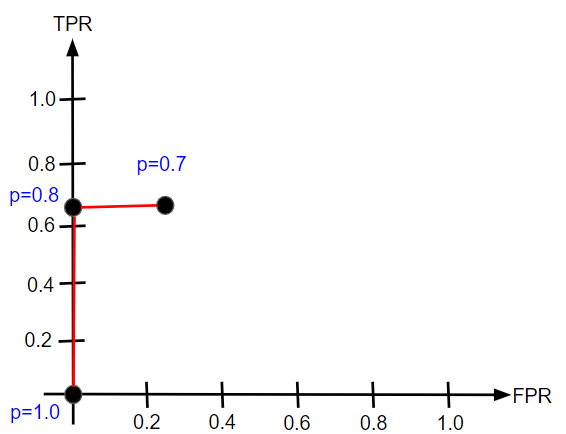
ROC曲線の書き方掴めてきたでしょうか?
同じような要領で閾値を変えながらROC曲線を描いていくと、完成形は次のようになります。
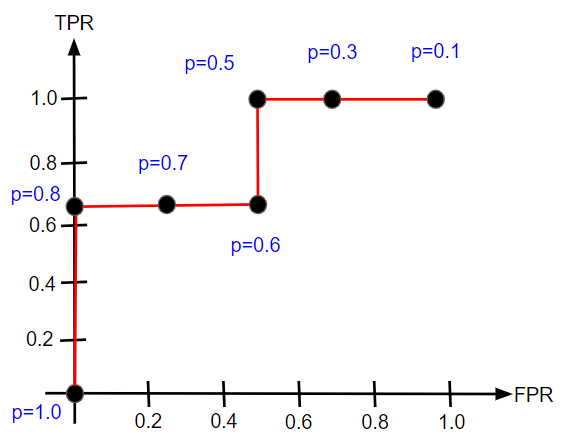
これでROC曲線を描けましたが、ここから何が分かるのでしょうか?
最初にも言った通り、よいモデルであれば閾値以上では全て陽性、閾値未満では全て陰性になるはずです。例えば、以下のようになっていれば、閾値0.7で陽性・陰性がくっきり分かれます。

このようなケースではROC曲線は次のようになります。
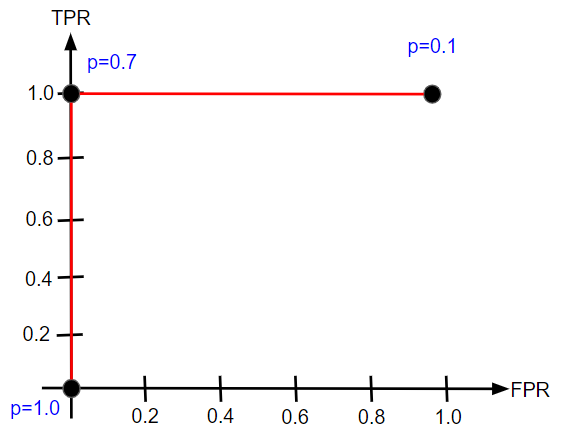
特徴としてはFPRの値が大きくなる前にTPRが1.0に到達しています。言葉で言えば、誤判定をすることなく、陽性の対象を全て陽性と判定できているということになります。これは理想的なモデルの場合ですが、一般化して言えばよいモデルはFPRが小さいうちにTPRが大きくなっていきます。
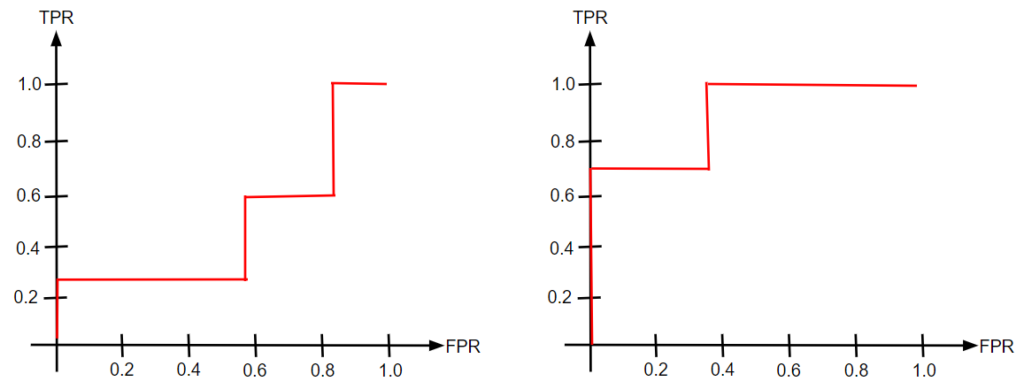
従って、以下のような2つのROC曲線を見れば、素早くTPRが立ち上がっている右の方がよいモデルであると判断することができます。
AUCとは?
ROC曲線が分かってしまえば、AUCはそれほど難しくはありません。
ROC曲線は見た目でモデルの良し悪しが分かりますが、見た目を基準にするのも若干曖昧なので、それを数値的な基準に直したのがAUCです。
では、ROC曲線の見た目をどのように数値化するのでしょうか?
それはずばりROC曲線が囲む領域の面積(下図の水色の領域)です。
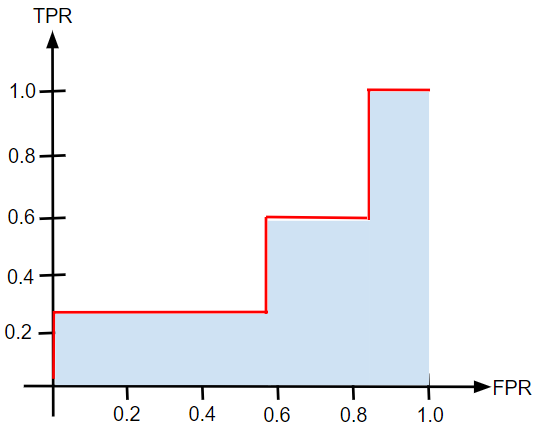
先ほどFPRが小さいうちにTPRが立ち上がる(大きくなる)のがよいモデルの特徴だと言いました。そのようなモデルではROC曲線が囲む領域の面積が大きくなります。繰り返しの掲載ですが、ROC曲線を2つ並べた以下の図を見てもらえば明らかだと思います。よいモデルである右の方が面積は大きいですね。
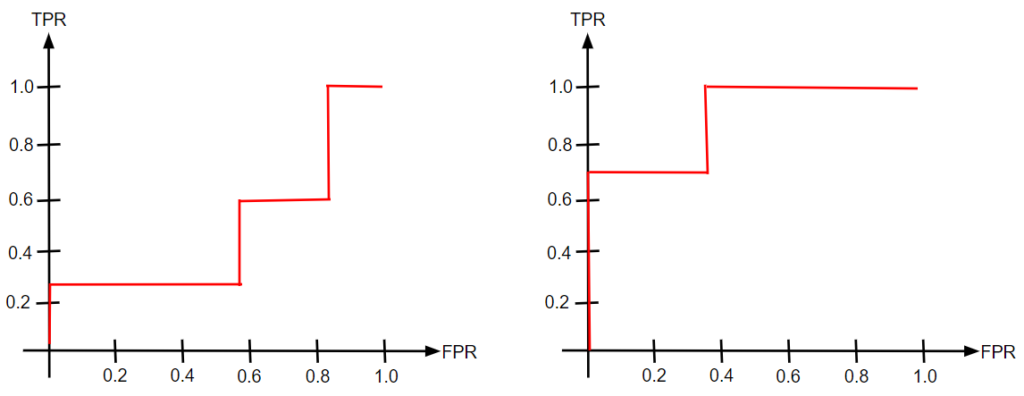
ちなみに、以下のような理想的なモデルでは1辺の長さが1の正方形ができますので、AUCの値は1になります。つまり、AUCが1に近いほどよいモデルであるということもできます。
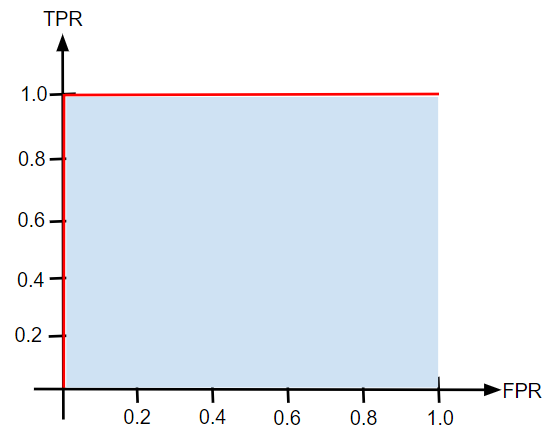
このようにAUCを導入することで数値的に曖昧さがなくモデルを評価することができるようになります。
最後に
今回は二値分類問題のモデル評価に役立つROC曲線とAUCについて解説をしてみました。
私もそうでしたが、始めのうちはROC曲線の書き方が少しややこしく感じるかもしれませんね。この記事では1歩1歩順を追って解説したつもりでしたので、初心者の方の助けになれば幸いです!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!













