【かみ砕いて説明します】ロジスティック回帰分析を分かりやすく解説

今回はロジスティック回帰を取り上げてみたいと思います。

ロジスティック回帰は二値分類問題を解く際に頻繁に用いられる分析方法です。

「回帰」と呼ばれていますが、実際は「分類」に用いられるという点に注意しましょう。

以前解説をした線形回帰に比べると用いる数式が少し複雑なこともあり、少し分かりづらいので、線形回帰と比較しながら1つ1つ丁寧に解説していきたいと思います。

線形回帰を忘れてしまった方は是非↓の記事を参照してみて下さい。

講師への質問OK! 16時間で学べるG検定対策講座【チートシート付き】

ロジスティック回帰の対象は二値分類問題

ロジスティック回帰では二値分類問題を対象としています。

二値分類問題とは入力に対してYes/Noのラベルをつけるようなタスクのことです。例えば、犬の画像分類タスクでは、入力された画像が犬であるかどうかという問いに対して、YesまたはNoを返します。スパムメールのフィルタリングであれば、届いたメールがスパムかどうかという問いに対してYes/Noを返します。このようなタスクが二値分類問題です。

線形回帰では1次式に入力を渡すと、それに対応した出力（数値）が返ってきますが、今回のロジスティック回帰は入力を渡すとYes/Noのラベルを返すようにしなければなりません。

では、ロジスティック回帰ではどのような関数（数式）を用いるのが適切なのでしょうか？

ロジスティック回帰はシグモイド関数を使う

先に結論を述べると、ロジスティック回帰ではシグモイド関数を使用します。

あまり聞き慣れない関数だと思うので、まずはその形から確認しましょう。

$y=\frac{1}{1+e^{-x}}$

$e$はネイピア数と呼ばれる特殊な数値です。今回は詳細を割愛しますが、シグモイド関数には次のような性質が備わっています。

シグモイド関数の性質

$x$が$0$の時は$0.5$になる
$x$が大きくなると$1$に近い値になる
$x$が小さくなると$0$に近い値になる

これらの性質をグラフで表現すると以下のようになります。

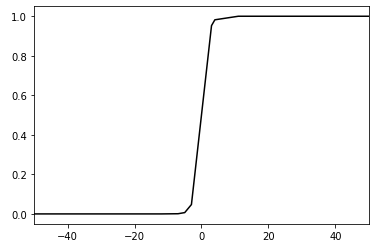
ここまでがシグモイド関数の説明になりますが、なぜこのような耳慣れない関数を使うことが二値分類問題を考えるのに便利なのでしょうか？

シグモイド関数の出力は確率と考えよう

グラフを見て分かるようにシグモイド関数の値は必ず0～1のどこかになります。つまり、シグモイド関数の出力値は確率だと解釈することができるのです。

分かりづらいかもしれないので、具体例を挙げてみましょう。

例えば、スパムメールの判定で、あるメールをシグモイド関数に渡したら$0.7$という値が返ってきたとします。これは、そのメールが70%の確率でスパムだと判定されたと解釈することができます。繰り返しになりますが、シグモイド関数の値は必ず0～1の間なので、常にこのような解釈が成り立つのです。

ただ、最初に述べたように、二値分類問題ではYes/Noのようなラベルを返すのが目標です。そこで、予めYesまたはNoと判断する確率の閾値を決めておきます。例えば、確率が50%を超えたらYesと考えようといったルールです。このようにしておけば、シグモイド関数の値が$0.8$の時はYes、$0.3$の時はNoといったように考えることができます。

ちなみに、閾値はタスクの目的によって変わります。例えば、「スパムは絶対に見逃したくない」ということであれば、Yesと判定されやすいように閾値を低めに設定します。逆に「うっかり普通のメールをスパムだと誤解するのは避けたい」ということであれば、Noと判定されやすいように閾値は高めに設定します。