今回はMobileNetの要点を初心者にも分かりやすく解説していきたいと思います。
開発の経緯から技術的な特徴まで順を追って進めていきます!
なぜMobileNetが開発されたのか?
これまでこのブログで紹介してきたAlexNet、VGG、GoogleNet、ResNetなどは、基本的には性能が向上するにつれて、ニューラルネットワークの層もより深くなっていました。
性能が向上することは喜ばしいですが、層が深くなれば、モデルのパラメータや計算量も増えていくので、CPUやメモリなどの必要となるリソースも増大していきます。
しかし、実際にはリソースは有限なので、いくら性能がよくても、あまりにスケールの大きいモデルは扱うのが困難になってしまいます。
このような背景を踏まえて、従来並みの性能を持たせつつ、計算量を抑えたモデルを作ろうということで開発されたのがMobileNetです。
スマホなどのモバイル機器でも扱えるようなモデルということで、MobileNetと名づけられました。
MobileNetの特長
MobileNetの特長は、ここまででも述べたように、計算量を減らすための工夫です。
その工夫は、Depthwise Separable Covolution(デプスワイズセパラブルコンボリューション)と呼ばれる畳み込みの計算です。
ここからは、このDepthwise Separable Convolutionを解説していきますが、より明快に理解していただくために、まずは通常の畳み込み計算の確認から入りましょう。
通常の畳み込み計算(確認)
後で説明するDepthwise Separable Convolutionを理解しやすくするために、ここではまず通常の畳み込み計算を確認しておきます。
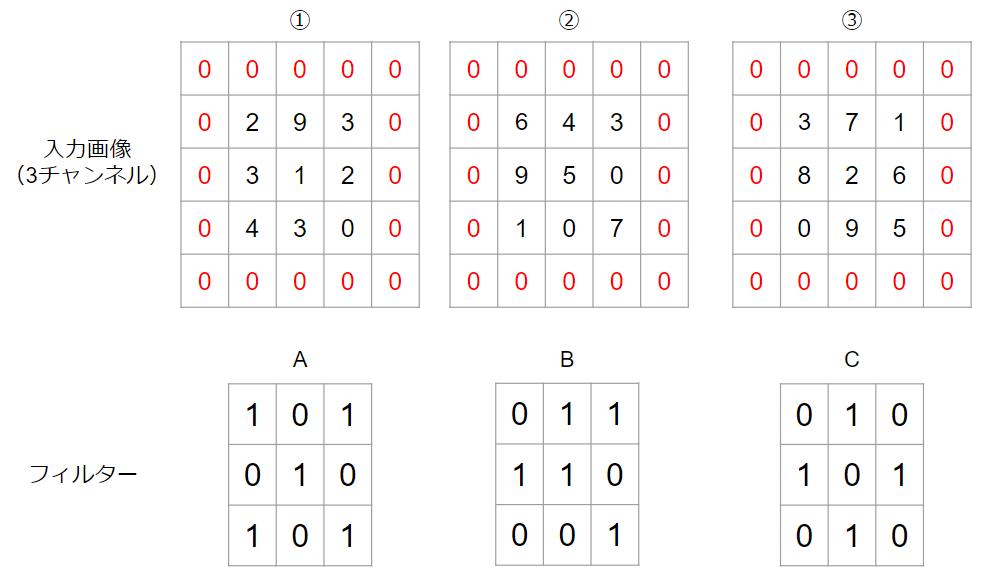
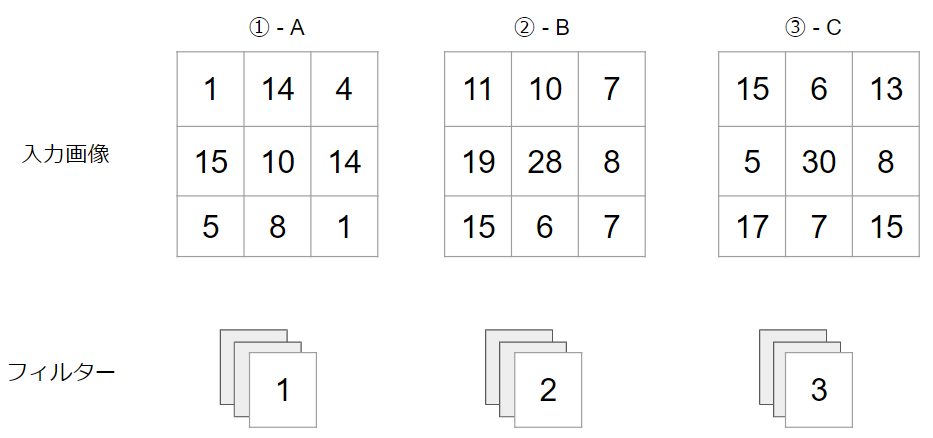
上記のように3チャンネルの入力画像がある場合を例にして考えます。画像周囲の赤色のゼロはパディングです。パディングをご存じない方は↓も読んでみてください。
このような場合には、①とA、②とB、③とCで畳み込み計算を行って、その結果を足し合わせます。実際にやってみましょう。
まずは、①とAで畳み込みです。
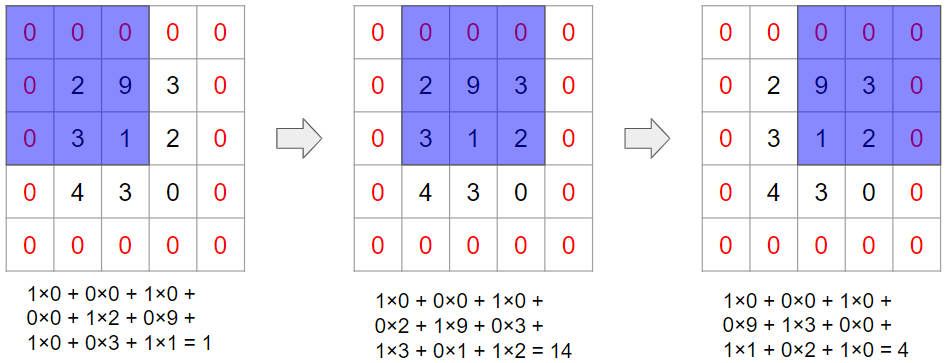
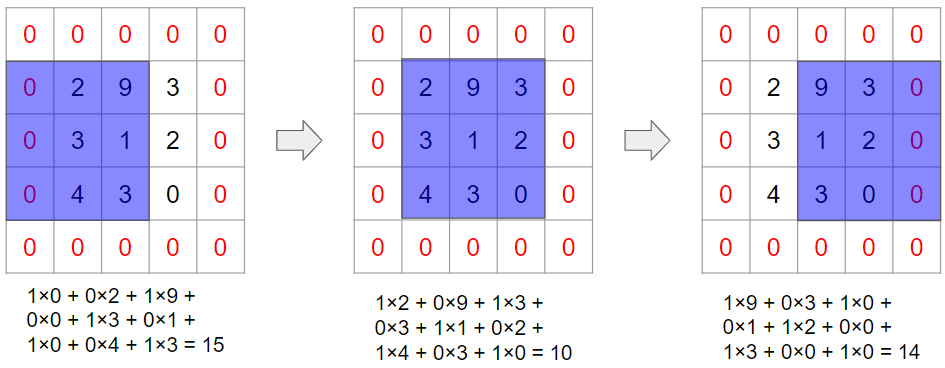
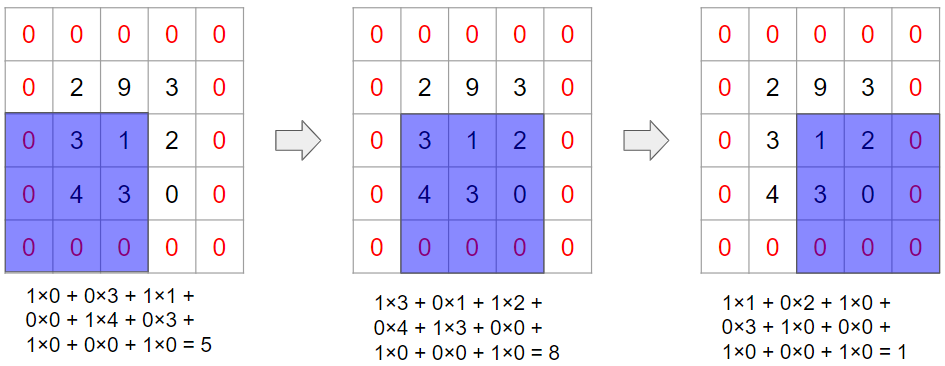
①とAの畳み込み計算の結果として、以下の出力を得ます。
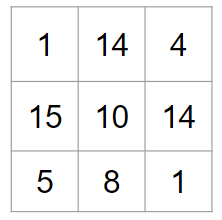
ここで後々のために、上記の計算の計算量を確認しておきます。
まず1回フィルターを適応すると、フィルターのサイズ分だけ乗算が発生します。今回の例で言うと、3×3=9回です。そして、フィルターを順次ずらして計算してきますが、フィルターを動かす回数は入力画像のサイズと一致します。今回の例で言えば、入力画像のサイズはパディングを除いて3×3なので、フィルターの移動回数は9回です。
つまり、入力画像を$D_{F}$、フィルターサイズを$D_{K}$とすると、1回の畳み込みを行なうのに、$(D_{F}×D_{F}×D_{K}×D_{K})$回の計算が発生します。今回の例で言うと、9×9=81回の計算をしています。
今回は入力チャンネルが3つあるので、同じ計算を3回行なって、次の結果を得ます。入力チャンネル数を$M$とすると、この時点で計算量は$(D_{F}×D_{F}×D_{K}×D_{K}×M)$回です。今回の例で言えば、9×9×3 = 243回です。
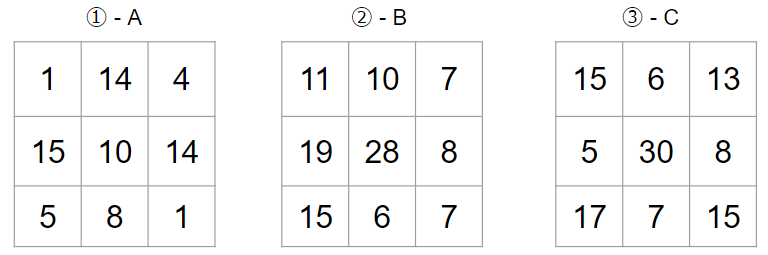
最後にこれらを足し合わせて、畳み込み計算が完了します。
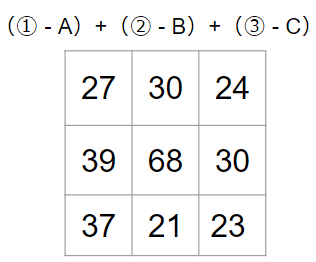
今回の計算の結果は1チャンネルになりましたが、複数チャンネルの出力を得たい場合もあります。その際には、フィルターのセット(今回の例で言うと3枚)を増やします。
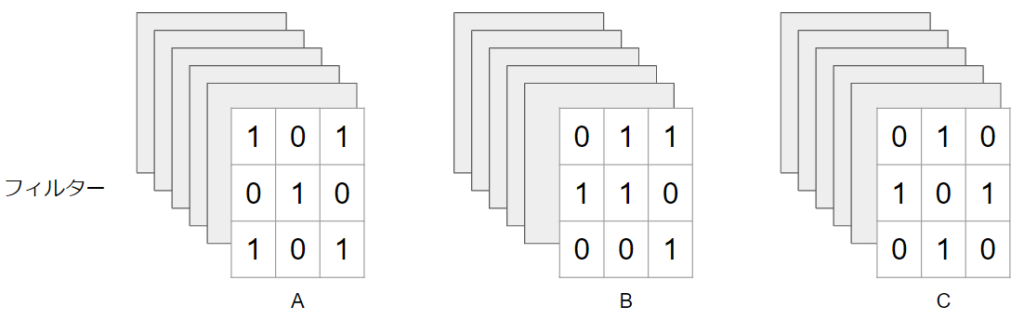
仮にフィルターのセットが$N$チャンネルあるとすれば、ここまで説明した計算を$N$回行うので、最終的な計算量は$(D_{F}×D_{F}×D_{K}×D_{K}×M×N)$回です。
最後にもう1度計算量の数式をまとめて掲載しておきます。(※パディングは省略しています)
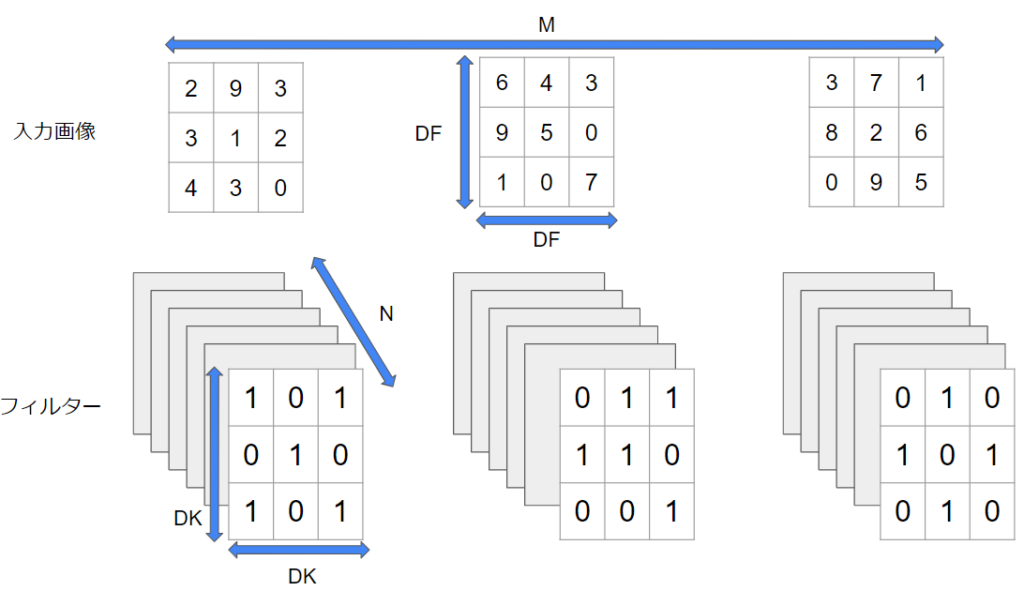
$D_{F}×D_{F}×D_{K}×D_{K}×M×N$
$D_{F}$:入力画像の縦・横のサイズ
$D_{K}$:フィルターの縦・横のサイズ
$M$:入力画像のチャンネル数
$N$:出力画像のチャンネル数
Depthwise Separable Convolution
では、ここから本題のDepthwise Separable Convolutionを説明していきます。
Dpethwise Separble Convolutionは、実はDepthwise Convolution(デプスワイズコンボリューション)とPointwise Convolution(ポイントワイズコンボリューション)に分割できます。従って、これらを2つに分割して、順に説明していきます。
先ほどの例と近しいシチュエーションで具体的に考えていきます。
- 入力画像の縦・横サイズ:3×3
- フィルターのサイズ:3×3
- 入力画像のチャンネル数:3
- 出力画像のチャンネル数:3
Depthwise Convolution
Depthwise Convolutionでは、入力画像のチャンネル数と同じだけフィルターを用意します。今回の例で言えば、フィルターは3枚になります。
従来の考え方であれば、出力チャンネル数も加味して、$M×N$枚(今回の例では3×3の9枚)が必要ですが、出力チャンネル数についてはPointwise Covolutionで考えるので、ここでは考慮不要です。
そうすると、以下のような状況になります。(※パディングは省略しています)
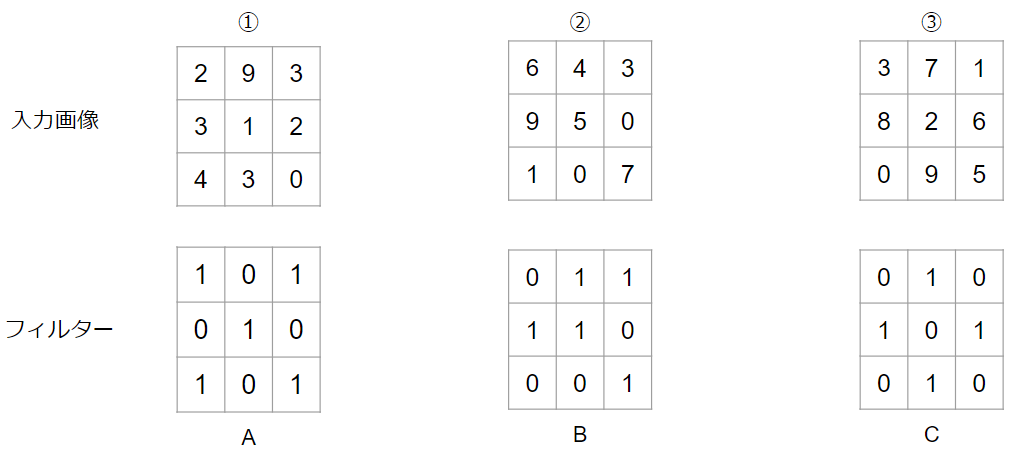
この畳み込みはすでに先ほどの例でやっており、以下のような結果になります。(同じ結果の再掲です)
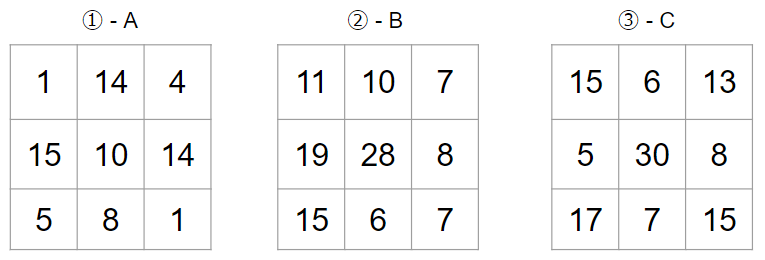
なお、ここまでの計算量は$(D_{F}×D_{F}×D_{K}×D_{K}×M)$回です。フィルターは入力画像のチャンネル数に合わせて1セットしか用意しておらず、言ってみれば出力チャンネル数$N=1$の状態なので、畳み込みの計算量の公式に$N=1$を代入すれば算出できます。
Pointwise Convolution
Pointwise Convolutionは一般的に1×1のフィルターを用いた畳み込みを意味します。
このMobileNetにおいては、1×1のフィルターを入力チャンネル数×出力チャンネル数(今回の例では3×3=9枚)だけ用意します。
Pointwise Convolutionにおける計算量を考えてみましょう。ここでは、フィルターサイズが1×1なので、計算量の公式において$D_{K}=1$の状態です。従って、計算量は$(D_{F}×D_{F}×M×N)回$です。
計算過程は従来の畳み込みと同様なので省略しますが、このPointwise Convolutionの結果として、3×3の画像を3チャンネル分出力として得ることができます。
Depthwise Separable Convolutionの計算量はDepthwise ConvolutionとPointwise Convolutionの計算量を足せばよいので、以下のように書き表すことができます。
$D_{F}×D_{F}×D_{K}×D_{K}×M ~ + ~ D_{F}×D_{F}×M×N$
$D_{F}$:入力画像の縦・横のサイズ
$D_{K}$:フィルターの縦・横のサイズ
$M$:入力画像のチャンネル数
$N$:出力画像のチャンネル数
では、従来の畳み込み計算とDepthwise Separable Convolutionで計算量を比較してみましょう。先ほど示した以下の例を前提として、上記で導いた公式に当てはめます。
- 入力画像の縦・横サイズ:3×3
- フィルターのサイズ:3×3
- 入力画像のチャンネル数:3
- 出力画像のチャンネル数:3
従来の畳み込み
$3×3×3×3×3×3 = 729$回
Depthwise Separable Convolution
$3×3×3×3×3~+~3×3×3×3 = 324$回
今回の例では、Depthwise Separable Convolutionにおいて、計算量を半分未満になることがお分かりいただけたかと思います。
MobileNetではこのようにして計算量を削減することで、軽量のモデルを実現しています。
Width MultiplierとResolution Multiplier
最後に補足でWidth MultiplierとResolution Multiplierという2つのパラメータを紹介しておきます。
MobileNetの特長は軽量化であると繰り返し述べていますが、軽量化をより一層促進させるのがこの2つのパラメータで、それぞれ以下の役割があります。
- Width Multiplier:入出力のチャンネル数を調整する
- Resolution Multiplier:入出力のサイズ(解像度)を調整する
実際にこれら2つのパラメータを適用した後の計算量の数式は以下のようになります。
$ρD_{F}×ρD_{F}×D_{K}×D_{K}×αM ~ + ~ ρD_{F}×ρD_{F}×αM×αN$
$D_{F}$:入力画像の縦・横のサイズ
$D_{K}$:フィルターの縦・横のサイズ
$M$:入力画像のチャンネル数
$N$:出力画像のチャンネル数
$α$:Width Multiplier($0 \leqq α \leqq 1$)
$ρ$:Resolution Multiplier($0 \leqq ρ \leqq 1$)
なお、論文では、$α$や$ρ$を小さくすることにより軽量化が達成される一方で、若干精度が犠牲になることも報告されています。このように、精度を軽量化がトレードオフの関係にあることは覚えておくとよいでしょう。
以上、MobileNetの要点を簡単に説明させていただきました!
最後になりますが、より詳しく学んでみたいという方はAIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!