今回は機械学習のモデル評価に使える赤池情報量規準(AIC)取り上げてみたいと思います。
モデルの複雑さと精度のバランスを評価するための指標
これまで混合行列やROC曲線などモデルの性能を評価する指標を紹介してきましたが、今回は性能に加えてモデルの複雑さという側面も評価できることが特長です。
ここではまずモデルの複雑さとはどういうものかを説明し、そのうえでAICの中身を見ていきたいと思います。
モデルの複雑さとは?
モデルの複雑さの概念を理解するために回帰問題を取り上げてみます。次のようなデータを説明するための回帰曲線を求めたいとします。
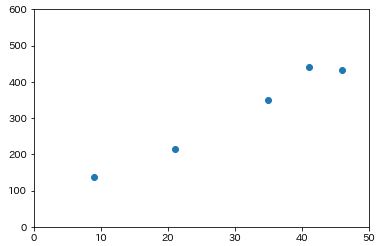
回帰曲線と書きましたが、最も単純なのは次のように直線で近似することなので、まずはそれを考えます。
$y = a_{1}x+a_{0}$
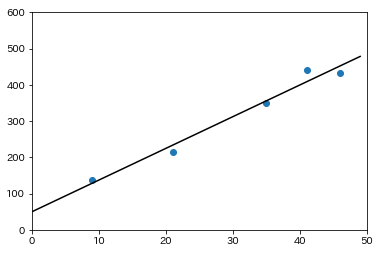
直線で近似をするということは、上記の数式に含まれる$a_{0},a_{1}$を求めるということなので、直線のモデルはパラメータが2つであるということになります。
この直線でもデータをよく説明できているように見えますが、さらにモデルを改良するために、今度は4次関数で近似することを考えます。
$y = a_{4}x^{4}+a_{3}x^{3}+a_{2}x^2+a_{1}x^1+a_{0}$
$a_{4}~a_{0}$まであるので、パラメータは5つです。それでは回帰曲線を描画してみます。
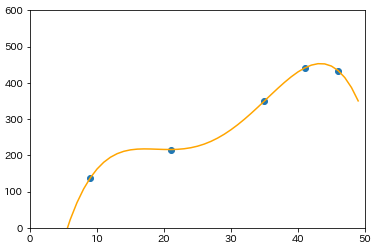
データの点を全て通るような曲線を引けたので、データを完全に説明できていることになります。
ここまで見てきて分かるように、パラメータが2つである回帰直線からパラメータが5つである回帰曲線にモデルを変更することで、データ点に対する近似精度を改善することができました。一般的にパラメータが多い方がモデルを柔軟に調整しやすいので、パラメータを増やすことによってモデルの精度を向上させることができます。
ただし、ここで注意すべきなのは、前者の直線のモデルよりも後者の多項式のモデルが必ずしもよいと言えないことです。なぜなら、パラメータが増えた分だけ、後者の方がモデルが複雑になったと言えるからです。
確かに精度がよいのは多項式ですが、我々がより簡単に理解できるのは直線の方です。また、(今回の例ではそれほど問題になりませんが)パラメータが増えることによって、計算をするためのリソース(CPUやメモリなど)をより多く消費することになります。
これがモデルの複雑さという観点です。繰り返しになりますが、パラメータが増えることによってモデルの精度は上がる傾向にあります。しかしながら、同時にモデルの複雑さも高まってしまいます。いくら精度が高くても複雑なモデルは扱いづらいものです。従って、モデルを設計する際には精度と複雑さのバランスを取ることが重要になるのです。
赤池情報量規準(AIC)とは?
AICはまさにモデルの複雑さと精度を同時に評価するための指標で、次式によって定義されています。
$-2\log{L} + 2k$
$L$は尤度(ゆうど)関数と呼ばれるもので、その対数を取ってマイナスを乗じたものは損失関数と言われます。ここでは損失関数や尤度の詳細説明は省きますが、回帰問題においては、損失関数はデータとモデルの予測値との差を表すと考えることができます。従って、モデルの精度が高ければ損失関数は小さくなります。
一方で、$k$はパラメータの数を表します。つまり、第二項目はパラメータの数が増えれば大きくなっていきます。
一般的に言って、AICの値が小さい方がよいモデルであると言えます。なぜなら、第一項目が小さければモデルの精度が高く、第二項目が小さければパラメータの数が少ない、つまりモデルが単純であると言えるからです。
先ほどの直線回帰と多項式回帰の例で考えると、多項式にすることで精度は上がったものの、パラメータが増えてモデルが複雑化しているので、AICの観点ではあまり改善しているとは言えません。
このようにAICを用いることでモデルの精度と複雑さをバランスよく評価することができます。
最後に
今回はモデル評価をする際に使われる情報量として知られている赤池情報量規準を解説してみました。
もしどうしても難しいと感じる場合には、数式はさておき、「モデルの精度と複雑さをバランスよく評価できる」という点だけでも頭に入れていただければと思います!!
最後になりますが、より詳しくAIを学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!












