【初心者向け】次元の呪いとは何なのか？

機械学習を学んでいると、次元の呪いというワードが比較的初期に登場してくるかと思います。私自身も機械学習の勉強を始めた頃に出会いました。ただ、名前自体の分かりにくさもさることながら、初期段階ではイマイチ内容を理解できずスルーしてしまう方も結構いらっしゃるのではないでしょうか？私もその口で後々振り返って少しづつ分かるようになってきました。

今回は、私のように次元の呪いを消化不良のまま機械学習の勉強を進めている方のために、次元の呪いを簡潔に説明してみました。皆さんの理解に少しでも役立てば幸いです。

【給付金で70%OFF】AI・データサイエンスの全コンテンツが期間無制限で見放題のキカガク長期コースの無料WEB説明会

Table of Contents

次元の呪いは2種類に大別することができる

そもそも次元の呪いとは、機械学習に用いるデータの属性数（＝次元）が大きくなった時に発生する問題のことを指しています。

そして、それは大きく2つの問題に大別することが可能で、その2つとはData sparsityとDistance concentrationです。

この2つの観点から次元の呪いを説明してみます。

Data sparsity（データの希薄性）

このData sparsityはデータの属性が増えれば増えるほど、様々な属性を持つデータを網羅的に集めるのが困難になるということです。

一般論では少し分かりにくいかもしれませんので、具体例を見てみましょう。例えば、顧客がある商品Aを買うかどうかを顧客の年齢と性別から機械学習を使って予測するというタスクを実行するとします。この時、年齢についてはyoung/adult/senior、性別についてはmale/femaleという選択肢があるとします。そうすると、起こり得る顧客のパターンは次の6通りになります。

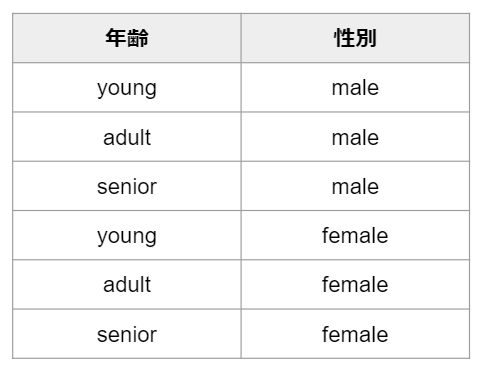
機械学習では学習を行なう際に多様なデータを用いることが予測精度を上げるために非常に重要です。例えば、学習時に男性のデータばかりを用いてしまうと、実践で用いるとなっても女性のデータに対しては全く使えないといったことが起こり得ます。従って、今回の例の設定であれば、学習時に6パターン全てのデータを集めてバランスよく学習に用いることが理想です。

では、ここで予測に使うデータの属性に未婚（single）/既婚（married）を追加するとしましょう。今度は顧客のパターンが増えて次の12通りになります。

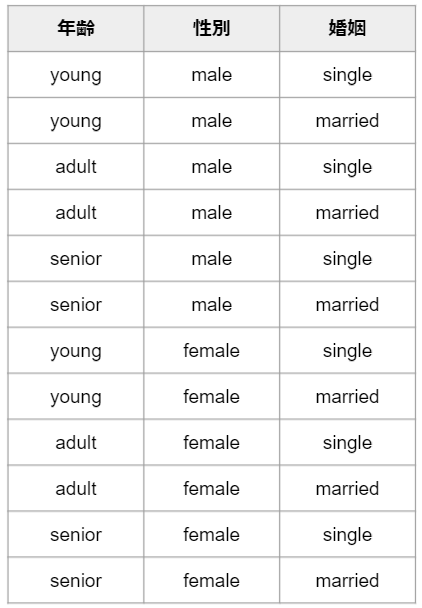
このケースでも先ほどと同様の考えで、全ての顧客のパターンを網羅して機械学習を行なうことが望ましいと考えると、データは最低でも12パターン必要になります。先ほどデータ属性が2個だった時には最低6パターンのデータがあればよかったものがデータ属性が3個になって最低限必要なデータ数が増えましたね。

このようにデータ属性が増えれば増えるほど、全てのパターンを網羅するのに必要なデータ数はどんどん増えていきます。必要なデータ数が増えるということはデータを集める労力が増えていくので、機械学習を行なうためのハードルが上がっていきます。一方で、データを集めることを怠れば、偏ったデータで学習してしまうことになるので、よいモデルを得ることはできません。

これこそが次元の呪いのData sparsity（データ希薄性）と呼ばれる問題です。

Distance Concentration（距離集中）

こちらはData sparsityに比べると少し理解しにくいので、丁寧に説明していきたいと思います。

ここではデータのクラスタリング（データを似た者同士でグループに分けること）を考えます。例えばですが、4人の人間の身長と体重が次のような分布になっていた場合に、皆さんはこの4人をどのようにグループ分けしますか？

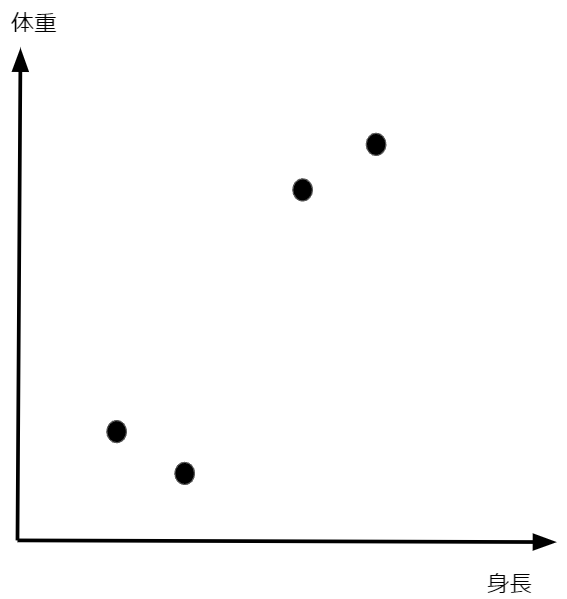
Distance Concentrationの説明（データの距離に基づくクラスタリング）

おそらく直感的に以下のような2グループ（赤枠と青枠）に分ける場合がほとんどだと思います。

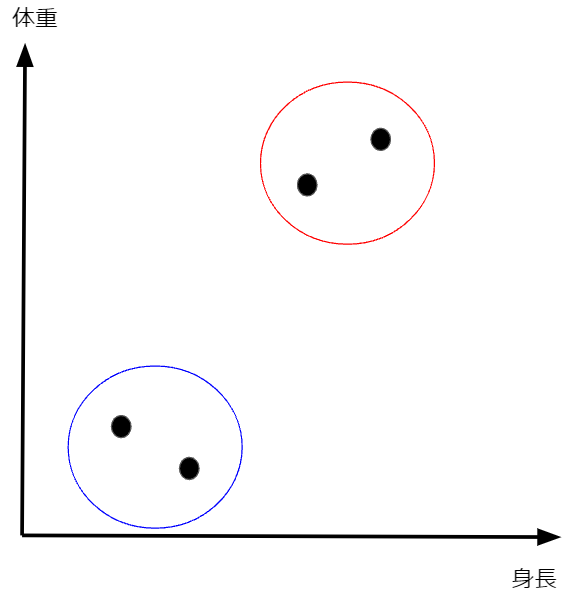
このようなデータを見た時に皆さんが直感的に分類をすることができたのはなぜでしょうか？それは青枠の点と赤枠の点では点同士の距離が離れているため、明らかに違う性質のものだと見なせるからだと思います。すなわち、この例から言えることは、データのクラスタリングにおいては2点間の距離が非常に重要な役割を果たすということです。

さて、ここから本題のDistance Concentrationの話に入っていこうと思います。少し抽象的な例になってしまいますが、属性Aと属性Bをもつ以下のような4つのデータ存在するとします。

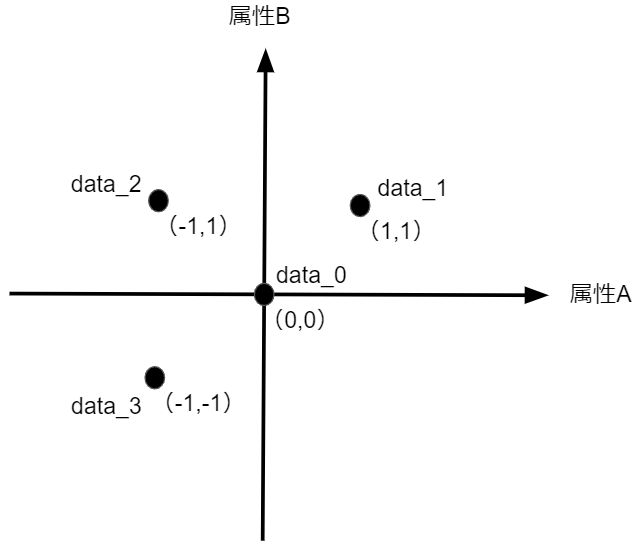
このデータを直感的に捉えるのであれば、各点は全て異なる象限にあるので、異なる部類のデータだと考えることができるでしょう。一方で、このデータを先ほどの距離の考え用いてクラスタリングすることを考えてみましょう。data_0を基準として各データまでの距離を算出すると、全て $\sqrt{2}\\$ になりますね。ということは、data_0から見た場合にdata_1～data_3は全て等距離にあるため、分類上は全て同じグループのデータということになります。繰り返しになりますが、直感的には異なるデータであるにも関わらず、距離が同じであるために、あたかも同類のデータであるかのように見えてしまっているということですね。

今回はdata_1～data_3までの3点を例に挙げましたが、これは半径が$\sqrt{2}\\$の円周上にあるような点であれば全く同じことが起こります。つまり、非常に多くの点で同様の現象が起こり、今の例のように適切な分類が困難になるということですね。

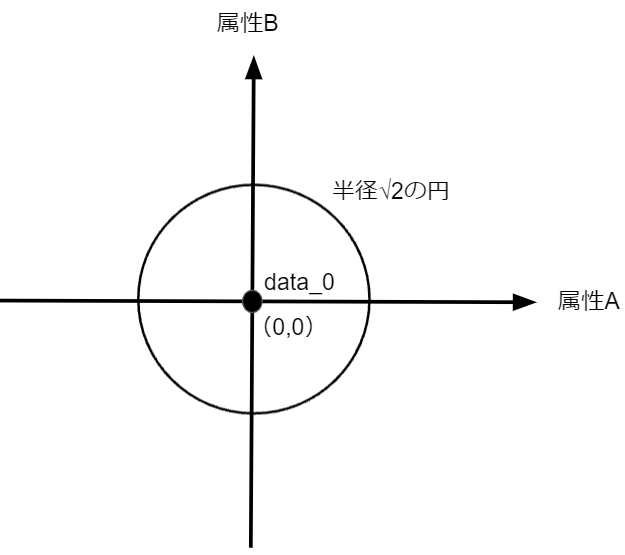
さて、ここで次元を1つ落としてみます。ここまでは、属性A・Bの2次元でしたが、属性Aの1次元で考えてみようと思います。この場合はdata_0から見て、距離が$\sqrt{2}\\$となる点は2つしか存在しませんね。

つまり、次元を落としたことで等距離に点が発生してしまうパターンがグッと少なくなったということです。

さて、ここまでの話をまとめてみます。データのクラスタリングにおいては、データ間の距離によってデータの同質・異質を判定していました。言い換えれば、データ間の距離が同じであれば、実際は異質であっても、あたかも同類のデータであるかのように判別されてしまうこともあり、クラスタリングの難易度が上がるということです。今回の例では1次元と2次元で、データは異質であるにも関わらず、距離が等しくなってしまう点がどれくらい発生しやすいかを見てみました。結果的には次元が2次元に増えたことによって、距離が等しくなってしまう点が発生しやすいということがお分かりいただけたかと思います。

これが次元の呪いのDistance Concentrationが意味するところです。今回は1次元と2次元の比較でしたが、さらに次元が上がっていくと、この傾向は顕著になっていき、非常に高次元な空間（すなわちデータの属性がとても多い）においては、データ間の距離はほとんど一定値になってしまうことが知られてます。