今回はディープラーニングの基礎であるニューラルネットワークを取り上げたいと思います。
人間の脳の働きを数値的にモデル化したもの
我々は人口知能に分類や回帰などの問題を解かせようとしていますが、それを日常的に行なっているのが人間です。例えば、我々は写真を見た時に「これは猫だ」「これは飛行機だ」のように瞬時に判断することができます。人間がやっていることを人工知能にやらせるのだから、人間の脳の働きをプログラムで再現すればよいという発想ですね。
人間の脳をモデル化すると聞くと、非常に難しそうに感じるかもしれませんが、ここではゼロから分かりやすく説明していきます。ディープラーニングへの第1歩を踏み出しましょう。
人間の脳の働きとは?
ニューラルネットワークは人間の脳の働きをモデル化したものなので、まずは人間の脳から理解していきましょう。と言っても、(私を含めて)ほとんどの方は脳の専門家ではないと思うので、医学的な専門知識は不要で、あくまでニューラルネットワークの理解に必要なところだけ押さえることができれば大丈夫です。
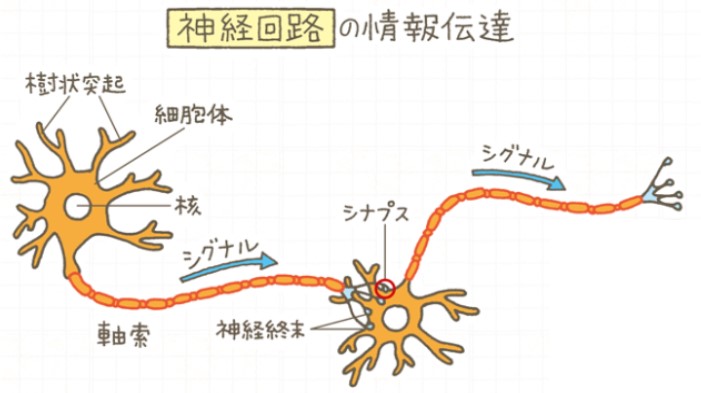
人間の脳にはニューロンと呼ばれる神経細胞が数百億個単位で張り巡らされており、これらが互いに情報を伝達しあうことで、高度な情報処理が可能になると言われています。
公益財団法人 東京都医学総合研究所 脳神経回路形成
ニューロンは情報を電気信号として受信すると、他のニューロンに対して受信した情報を伝達していきます。ただし、他のニューロンに渡す際に受け取った情報をそのまま流すのではなく、何らかの計算を行なったうえで伝達しています。これは数学的な表現をすれば、まさに関数です。入力$x$を関数$f$に通して、$y=f(x)$として出力していると考えれば、数値的に表現することは不可能ではなさそうです。
最もシンプルな単純パーセプトロン
では、早速ここまでで説明した人間の脳の働きをモデル化してみましょう。あまり難しいことは考えずに率直に表現してみると、例えば次のようになるでしょう。
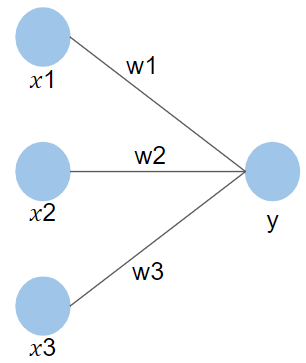
左側の各点(ノードと呼ぶ)が入力情報($x_{1}, x_{2}, x_{3}$)を受け取るニューロンで、それらが次のニューロンに情報を渡します。ただし、単に横流しするのではなく、一定の比率($w_{1}, w_{2}, w_{3}$)を掛け合わせて渡します。数式で表現すると、次のようになります。
$y = w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3} $
いきなり一般式で記述したので、もしかしたら分かりづらいと感じた方もいるかもしれませんが、具体例で表現すると次のようになります。
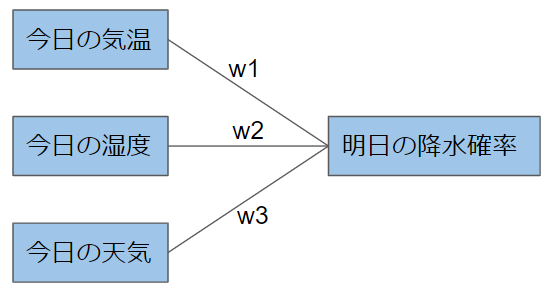
明日の降水確率=$w_{1}\times$(今日の気温)$+w_{2}\times$(今日の湿度)$+w_{3}\times$(今日の天気)
言葉で表現するならば、明日の降水確率を予測するのに、今日の気温・湿度・天気を比率(優先順位)をつけて考慮するということになります。例えば、今日の気温の影響が大きいと考えるのであれば、$w_{1}$が$w_{2}, w_{3}$と比べて大きくなります。
このような構造を持つニューラルネットワークのことを単純パーセプトロンといいます。そして、入力情報を受け取るノードを入力層、結果を出力するノードを出力層、情報を伝達する比率($w_{1}, w_{2}, w_{3}$)を重みと言います。
ただし、単純パーセプトロンはその名前が示すように構造が単純なので、複雑なタスクを行なうのには不十分です。従って、より複雑なタスクのために、このモデルをもう1歩拡張していきます。
活性化関数の導入
では、モデルの性能を向上させるための第1歩として活性化関数を導入します。
まずは、先ほどの具体例で考えてみましょう。具体例では出力が「明日の降水確率」でした。確率なので、出力は必ず0~1の値を取るようにしておくのが妥当です。このような目的からシグモイド関数を導入するのがよいと言えるでしょう。
※シグモイド関数を忘れてしまった方は是非↓の記事も読んでみて下さい。
シグモイド関数を導入すると、モデルは以下のように表現することができます。
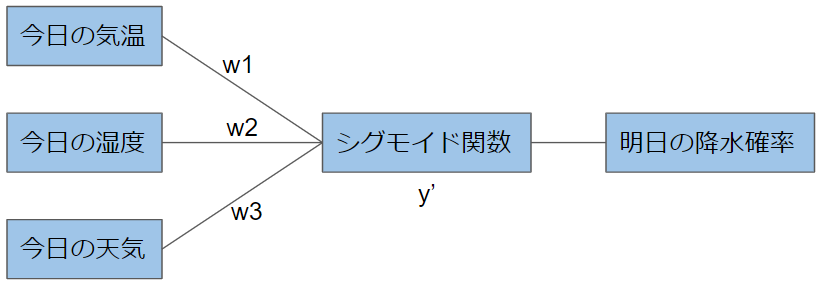
$y’=w_{1}\times$(今日の気温)$+w_{2}\times$(今日の湿度)$+w_{3}\times$(今日の天気)
明日の降水確率$= sigmoid(y’)$
このようにニューロンからニューロンへ情報を伝達する際には、重みと入力の掛け合わせだけでなく、関数による変換を加えるのが一般的です。理由は、このような関数を導入することによって、モデルがより複雑な思考を表現できるようになるからです。もう少し厳密な言い方をすれば、重みと入力の掛け合わせだけでは、単純な思考しか表現できず、実用的に用いることができません。このような関数のことを一般的に活性化関数と呼びます。今回の例では、シグモイド関数でしたが、それ以外にも様々な関数が使用されます。
最後に活性化関数を含めた一般的な図を以下に示します。活性化関数を$f$と表現しています。ただし、活性化関数はノードではないので、ノードとは異なる図形で表現しています。
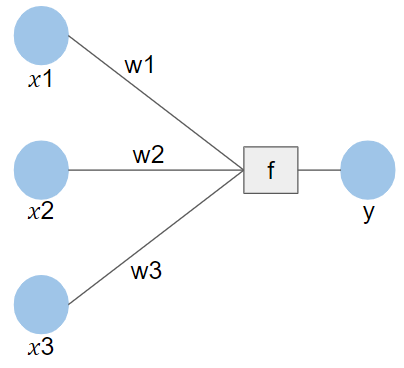
$y = f(w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3}) $
多層パーセプトロンへの拡張
ここまでは、入力層と出力層が直接つながった構造でしたが、その間にさらに層を追加してモデルを高度化していきます。層を追加すれば、より複雑な計算が可能なので、より複雑な思考を表現できるということです。
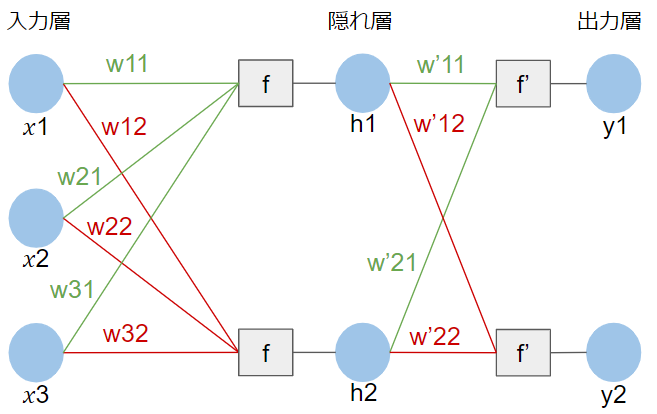
中間に$h$という層を挟み込みました。このような層は隠れ層または中間層と呼ばれます。見た目は随分と複雑になっていますが、ニューロンからニューロンへの情報伝達の流れに変更はありません。
まず、$h_{1}$と$h_{2}$への情報伝達は次のように表現されます。
$h_{1} = f(w_{11}x_{1} + w_{21}x_{2} + w_{31}x_{3}) $
$h_{2} = f(w_{12}x_{1} + w_{22}x_{2} + w_{32}x_{3}) $
式の形は単純パーセプトロンの場合と全く変わっていませんね。ちなみに、$h_{1}$と$h_{2}$へ向かう重みは異なってもよいので、$w$の添え字はそれぞれで違うものにしています。そして、今回は出力層のノードも増えていますが、やはり数式はこれまでと同様に考えることができます。
$y_{1} = f'(w’_{11}h_{1} + w’_{21}h_{2}) $
$y_{2} = f'(w’_{12}h_{1} + w’_{22}h_{2}) $
このように隠れ層を追加したモデルは多層パーセプトロンと呼ばれます。
今回は隠れ層が1つでしたが、もちろんタスクに応じてさらに追加することが可能です。ただし、気をつけなければいけないことは層が増えれば増えるほど学習するパラメーターも増えるということです。学習するパラメーターとは、学習を通して値を調整していく対象のことです。値がいい具合に調整されることによって、モデルの予測精度がどんどん上がっていくのです。
ニューラルネットワークでは重みが学習パラメーターです。ここまでの説明から分かるように、層を追加することによって重み$w$は増えていきます。学習パラメーターが増えるということは、メモリなどのリソースがより必要になるということを意味します。このような背景もあって、ニューラルネットワークは豊富なリソースが手に入りやすくなった近年に初めて注目を集めるようになりました。それ以前はSVMなどが機械学習の主流を担っていました。
最後に
今回はニューラルネットワークの基礎をできるだけ分かりやすく解説してみました。
途中で少し数式も登場しましたが、初めて学んだという方はまずはニューラルネットワークの構造を自分の中でしっかりイメージできるようになっていただければ幸いです!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!