今回は階層なしクラスタリングのK平均法を取り上げてみたいと思います。
データの重心点からの距離に基づいて、データをK個のグループにクラスタリングする分析方法
まず大前提としてK平均法は教師なし学習、その中でも階層なしクラスタリングに分類されています。そのため、データの特徴や構造を把握することが目的です。従って、数値を予測したり、画像を分類したりといったものではありません。定義が示すように、正解・不正解などはなく、与えられたデータをグループ分けする手法です。
今回は階層なしクラスタリングの意味を明確にしたうえで、K平均法が具体的にどういった手順でグループ分けを行なうのかを丁寧に解説してきます。
※教師なし学習に不安のある方は是非↓をご参照ください。
階層なしクラスタリングとは?
まずクラスタリングとは一言で言えば、グループ分けのことです。そもそもクラスターがグループを意味する単語なので、クラスタリングは与えられたデータの特徴に基づいて、その中にグループ構造を見つけ出すタスクと定義することができます。
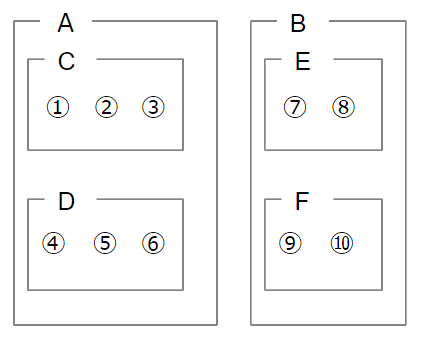
次に「階層なし」についてですが、階層というのはクラスタリングの多重構造のことを指します。具体例を出しましょう。手元に1~10まで番号が振られたデータがあり、これをグループAとグループBの2つに分類します。1~6までがA、7~10までがBに分類されたとしましょう。ここまでであれば、クラスタリングが1回行われただけなので、階層なしクラスタリングです。ここからさらに、グループAを1~3のC、4~6のDに、グループBを7,8のE、9,10のFに分けたとします。図で表現すると、以下のようにクラスタリングが多重構造になっているため、階層ありクラスタリングと呼ばれます。
繰り返し述べているように、K平均法は階層なしクラスタリングに属するので、多重構造を取らない形でデータのグループ分けを行ないます。
K平均法とは?
ここからは具体例を示しつつ、K平均法によってデータがどのようにクラスタリングされていくのかを明らかにしたいと思います。
冒頭にも述べたように、K平均法はデータをK個のグループに分けるのですが、Kの値は理論上はいくつでもOKです。Kの値は分析を始める前に決めておき、それに従って分析を進めていきます。ただし、理論上いくつでもいいとは言え、例えば「10個のデータを10グループに分ける」というのでは意味がないので、実用上はしっかり決める必要があります。グループ数を決めるアルゴリズムなどもありますが、基礎から少し遠のくので、今回の説明からは割愛します。
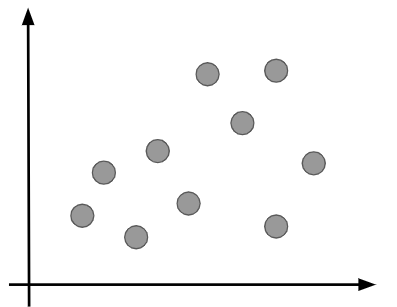
今回はこちらの10個のデータをK平均法で2つのグループに分ける(すなわちK=2)ことを考えてみたいと思います。
①代表点をKと同じ数だけ定める
まず座標上にKと同じ数だけ代表点を置きます。今回の例では2つの代表点が必要です。詳細は割愛しますが、実はこの最初の代表点の選び方によって、クラスタリングの最終結果が影響を受けてしまうことがあります。そのため、代表点を選ぶためのアルゴリズムも存在しますが、基礎レベルを逸脱するため、この場では言及しないことにします。今回は次のように代表点を置いたとして話を進めます。
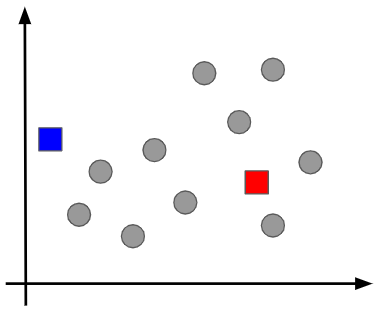
②代表点から各データ点までの距離に基づいて、データをクラスタリングする
先ほど代表点(青と赤の四角形)を決めましたので、その点から各データ点までの距離を調べます。その結果、青の代表点に近ければ青のグループに、赤の代表点に近ければ赤のグループにデータ点をクラスタリングをします。
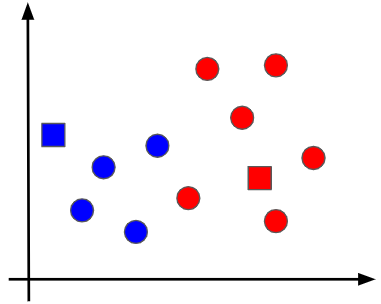
③各グループ内の重心点を求める
各データ点のクラスタリングができたので、同じグループに属するデータ点の間で、その重心点を計算します。厳密な計算方法は割愛しますが、重心点はデータ点が固まっている方向に寄っていく傾向があります。今回は重心点が以下のひし形の点として求まったとします。
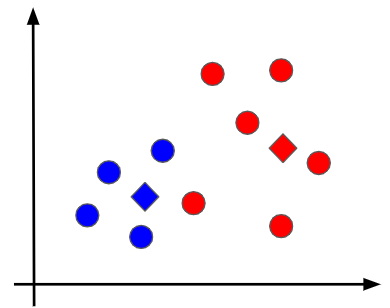
④各グループの重心点から各データ点までの距離に基づいて、再度データをクラスタリングする
ここは②の工程と同様に、青の重心点に近いデータは青のグループに、赤の重心点に近いグループは赤のグループに分類します。再度クラスタリングした結果が次の図です。中心の少し下辺りの点が赤から青に変わっていることに着目しましょう。赤の重心点よりも青の重心点の方が近くなったことが原因です。
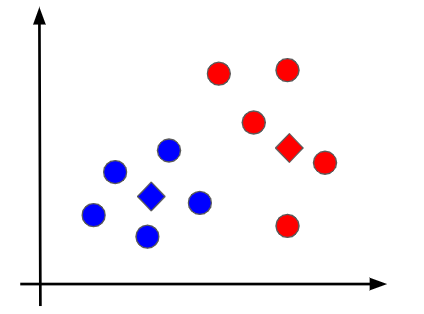
⑤③と④の工程を繰り返す
データを再度クラスタリングしたことによって、同じグループに属するデータ点に変更があったので、改めて各グループの重心点を計算します。つまり、③の工程を繰り返すわけです。新しい重心点が決まったら再び重心点からの距離に基づいて、クラスタリングをやり直します。これは④の繰り返しです。この流れを重心が変化なくなるまでひたすら実行します。
最後に
今回は階層なしクラスタリングであるK平均法を図を使いながら丁寧に説明してみました。
1回読んで分からなかったという場合でも、頭を整理して繰り返し読んでいたければ理解できると思いますので、理解できるまで何度も読み返してみて下さい!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!