【イメージで解説】主成分分析を分かりやすく解説します

今回は主成分分析を取り上げてみたいと思います。

主成分分析

データの本質的な特徴を抽出することによって、できるだけ情報量を保ったまま、高次元のデータを低次元に圧縮する分析方法

主成分分析も教師なし学習に分類されます。ただし、K平均法やウォード法のようにデータをクラスタリングするのではなく、データの特徴や構造を把握して次元削減することを目的としています。

今回はまず前提となる次元削減を説明し、その後で主成分分析やその他の次元削減の手法を紹介していきたいと思います。

なぜ次元を削減するのか？

主成分分析の内容に入る前に、まずは次元を削減することのメリットを明確にしておきましょう。

そもそも次元と言っているのは、データを説明するために用いる変数の数のことです。例えば、「今の気温と湿度から明日の天気を推定する」と言った場合には、明日の天気を説明するのに気温と湿度の2変数を使っているので、2次元だと言うことができます。明日の天気を仮にどちらか一方の変数で推定するとなれば、1次元となるので次元を削減したことになります。

それではここから次元削減を行なう3つの主なメリットを説明します。

①データを解釈しやすくなる

これはもう少しかみ砕いて言えば「データを理解しやすい」ということです。具体例で説明してみましょう。AさんとBさんという2人の人間の肥満度を比較するために以下のようなデータがあったとします。

	身長	体重	座高	胸囲	腹囲	運動時間	肥満度
Aさん	170cm	66kg	92cm	88cm	76cm	60分	高い
Bさん	170cm	64kg	90cm	89cm	77cm	30分	低い

この表を見た時に「なぜAさんがBさんより肥満度が高いと判定されたのか？」がぱっと分かるでしょうか？おそらく変数が多くて比較が大変だと思う方も多いのではないでしょうか。一方で、データが次のような形であればどうでしょう？

	身長	体重	肥満度
Aさん	170cm	66kg	高い
Bさん	170cm	64kg	低い

これであれば、同じ質問をされた時に「Aさんの方が体重が重いから」という答えがパッと出てくるのではないでしょうか。このようにパッと答えられたのは、変数が減ってデータが見やすくなったからですね。

このように変数が少ない方がデータの解釈がやりやすいため、次元は低い方がよいのです。

②データを可視化しやすい

データを扱う上でグラフ上に描画できるというのは非常に重要です。なぜならグラフを見ることによって、我々は直感的にデータを理解できるからです。

例えば、以下のような年齢と年収のグラフを見れば、瞬時に「年齢が上がるほど年収が増える傾向にある」ということは誰でも理解できます。

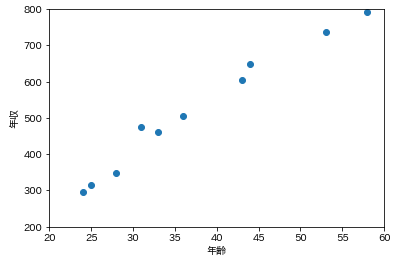
しかし、同様のデータを以下のような表で見せられると、上記のような傾向を瞬時に見て取るのは難しいでしょう。（もちろん表を上から下まで眺めれば分かるとは思いますが）

このような観点からデータの可視化は非常に重要なのです。ただ、残念ながら、データの可視化ができるのは3次元までです。4次元以上のデータはグラフで可視化をすることができません。従って、4次元以上のデータに出会った時には、何とかして2次元や3次元のデータにしたいというモチベーションが働きます。

③計算リソースを節約できる

機械学習を用いて回帰や分類の問題を解くと言った場合には、CPU/GPUやメモリと言ったリソースが必要になります。ほとんど説明するまでもないかもしれませんが、変数が少ない（＝次元が低い）方が必要となるリソースは少なくなります。言い換えると、同じリソースであれば、変数が少ない方が早く計算が終わります。

つまり、費用や時間という観点からも次元は低い方が得なのです。

次元削減をやってみよう

ここまでで次元削減のメリットは理解いただけたかと思いますが、変数を無作為に削減すればよいわけではありません。例えば、先ほどの肥満度を確認する例で言えば、いくら次元を削減したいからと言って、「身長だけ残して、あとは全て削除」としてしまっては、さすがに肥満度を確認することはできません。すなわち、特徴を捉えるのに不要な変数は消す、必要な変数は残すという判断をしなくてはなりません。

では、必要か不要かの判断はどのようにすればよいのでしょうか？

方法の1つとして、互いに関連性のある変数はどちらか一方を削除するという考え方があります。例えば、賃貸物件の家賃を以下の変数を用いて予測するというタスク（回帰問題）に取り組むとしましょう。

物件の面積
最寄駅からの距離
築年数
部屋の数
物件の竣工日

5次元のデータですね。確かにこれらの変数を用いて機械学習によって回帰問題を解くということも可能ではあります。しかし、この中には明らかに不要な変数があります。築年数と竣工日に着目してみましょう。例えば、築年数が5年ならば竣工日もほぼ5年前のはずです。築年数が10年なら竣工日もほぼ10年前のはずです。つまり、これらの2つの変数は表面上は異なるものであっても、どちらか一方が分かればもう一方もほとんど分かってしまうのです。従って、このような変数はどちらか一方を削ってしまっても本質的な情報量に影響ありません。

こういった変数が次元削減の対象になるのです。また、築年数と竣工日ほど明白ではなくても、面積と部屋数も互いに関係がありそうです。なぜなら、面積が大きい方が部屋数が多いという関連性が容易に想像できるからです。これはどんな場合でも絶対に正しいと言えるものではありませんが、概ねその傾向が成り立つのであれば、次元削減の対象になり得ます。

2つの変数の関連度合いを定量的に判断する指標として相関係数というものがあるので、この数値を参考にして削除するかどうかを決めることもあります。

主成分分析とは？

随分と前置きが長くなってしまいましたが、ここから主成分分析を説明します。

主成分分析は次元削減の手法の1つですが、上記で説明した例とは少し考え方が異なります。主成分分析はデータの中に潜む本質的な特徴量を抽出することによって次元を削減します。

抽象的な物言いで少し分かりづらいかもしれませんが、まずご理解いただきたいのは、先述の例のように、単に不要な変数を削除するというのとは考え方が異なるということです。

では、具体例を用いて説明していきましょう。例えば、気温と湿度を用いて周囲の環境の気候的な不快度合いを評価したいとします。直感的には気温・湿度ともに高ければ不快になりますし、気温が適切で湿度が低ければ快適に過ごせそうです。ここまでの話では不快度合いを温度と湿度の2つで評価しているので、変数は2次元ということになります。

ただ、実際には温度と湿度から計算される不快指数という指標で不快度合いを表せることが知られています。不快指数という1つの数値の大小さえ見れば、周囲の環境が不快かどうかが分かるということです。つまり、不快指数という本質的な特徴量を用いることで、変数を1次元に落とすことができたわけです。

数学的な詳細については基礎を逸脱するので割愛しますが、これが主成分分析の考え方です。

その他の次元削減の手法の紹介

主成分分析以外の次元削減の手法について簡単に紹介していきます。いずれも詳細には触れず、概念的な説明に留めたいと思います。

①特異値分解

特異値分解は主成分分析に非常によく似た手法です。与えられたデータから本質的な特徴量を抽出しようという考え方は同じです。ただし、計算過程で行なう行列計算が異なるため、互いに別の手法として認知されています。

②t-SNE

「ティースニー」や「ティースネ」と読みます。この手法では次元を圧縮した際にデータの関係性を保つことを非常に重視しています。例えば、3次元から2次元にデータを圧縮することを考えます。その際に、3次元空間上で距離が離れていたデータ同士は2次元に圧縮した際にも距離が離れているように、そして逆に3次元空間上で距離が近かったデータ同士は2次元に圧縮した際にも距離が近くになるようにするということです。

確かに次元を削減したことによって、データの関係性が変わってしまっては適切に次元を削減できているとは言えないので、納得のできる考え方ですね。

③多次元尺度構成法

これは同類のもの同士を比較する際に使われる手法です。例えば、複数のメーカーのノートパソコンを比較したい時に、各パソコン同士の類似度を考えます。ノートパソコンであれば、サイズ、バッテリーのもち、OS、価格、ハードディスク容量など比較に使える変数が様々思いつきますが、多次元尺度構成法では類似度という指標で製品同士の類似度合いを評価します。類似度は絶対的な指標でも単位を持つ指標でもなく、定性的な指標です。2次元のグラフにおいて、類似度が大きい（＝よく似ている）製品同士は近くに、類似度が小さい（＝あまり似ていない）製品は遠くに点を置くことで、製品同士の類似性を図示することができます。もともと多く存在した変数を類似度という指標に圧縮しているので、これも次元削減の一種です。