今回は階層ありクラスタリングのウォード法を取り上げていきます。
最も近接したクラスター同士で新たなクラスターを形成することによって、階層的なクラスタ構造を導き出す分析方法
定義から分かるように、ウォード法はデータをクラスター(グループ)に分けることを目的としているので、教師なし学習です。そして、その中でも階層ありクラスタリングと呼ばれる手法に属します。
ここでは階層ありクラスタリングの意味を明確にしたうえで、ウォード法の内容を直感的に理解できるように解説してきたいと思います。
※教師なし学習に不安のある方は↓もご覧ください。
階層ありクラスタリングとは?
まずクラスタリングとは与えられたデータをクラスター(グループ)に分けることです。教師なし学習がデータの特徴や構造を把握することを目的としているので、その一種であると言えます。
続いて、「階層」というのはクラスタリングの多重構造のことです。例えば、手元に1~10まで番号が振られたデータがあり、これをグループAとグループBの2つに分類します。1~6までがA、7~10までがBに分類されたとしましょう。ここからさらにもう1歩踏み込んで、グループAを1~3のC、4~6のDに、グループBを7,8のE、9,10のFに分けたとします。図で表現すると、以下のようにクラスタリングが多重構造になっているため、階層ありクラスタリングと呼ばれます。
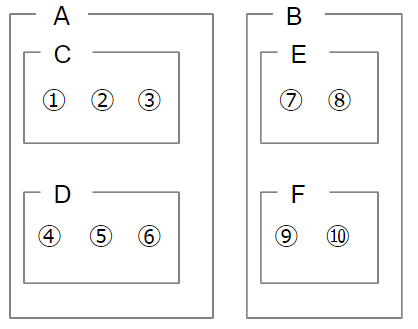
繰り返し述べているように、ウォード法は階層ありクラスタリングなので、結果としては上図のように多重構造のクラスタリンが得られることになります。
※階層なしクラスタリングの代表例であるK平均法は↓で説明しているので、もしよければ参考までにご覧ください。
ウォード法とは?
ウォード法でやる事はただ1つです。それは距離が最も接近している2つクラスター(またはデータ点)を組み合わせて新たなクラスターを作ることです。これをひたすら繰り返します。
理解を深めるために具体例を見てみましょう。今回は次の図の中にある6点をウォード法の考え方に沿ってクラスタリングしてみます。
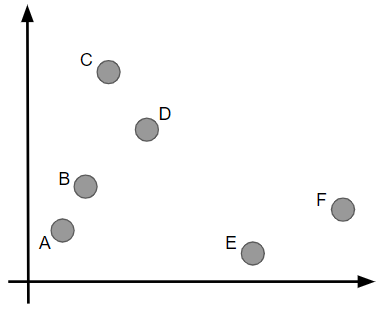
まずこれらの点の中から最も近接している2点を探します。AとBが最も近接していることが分かるので、これらを1つのクラスターとします。
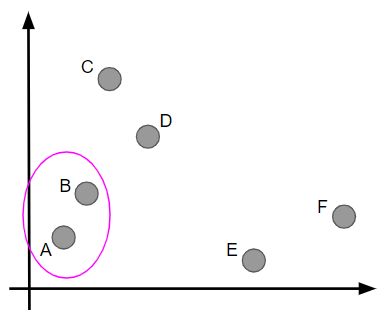
再び最も近接した2点を探します。今度はCとDがそれに該当するので、CとDをクラスターにします。
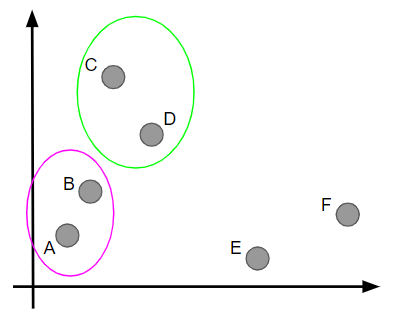
同様の考え方で今度はEとFでクラスターを形成します。
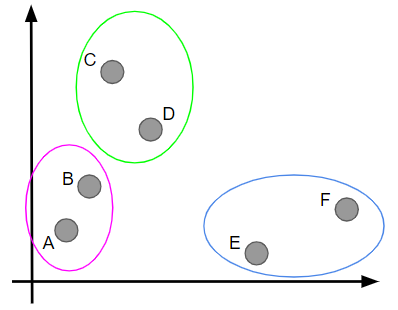
ここまでで全てのデータ点がいずれかのクラスターに属するようになりましたが、まだクラスタリングは続きます。考え方は同様で最も近接している2点を探します。ただし、点と言ってもABCDEFではなく、それぞれのクラスタの代表点(例えば重心など)を使って距離を考えます。そうすると、紫のクラスターと緑のクラスターが近接していることが直感的に分かると思いますので、これらが新たなクラスターとなります。
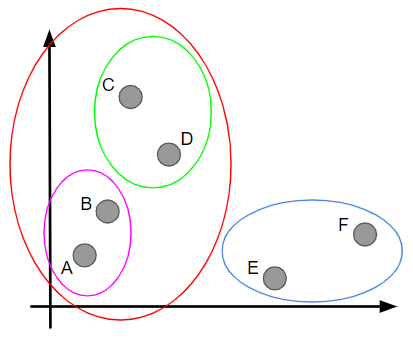
これでクラスターがABCDのグループとEFのグループの2つになりました。ここから新たにクラスターを形成するとしたら、この2つを組み合わせるしかないので、ここでクラスタリングが終了となります。
このクラスタリングの階層構造を樹形図を用いると次のように表すことができます。このような樹形図のことをデンドログラムと言います。
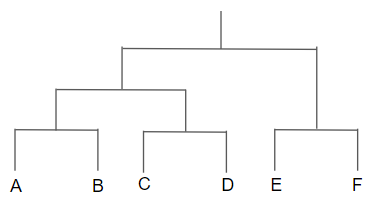
以上がウォード法によるクラスタリングの考え方になります。今回は概要を理解することを目的としていたので、データ点やクラスター間の距離の考え方についてはあまり詳しく触れず、図による直感的な把握のみに留めました。実際にはもう少し複雑な定義があるので、気になる方はぜひ調べてみて下さい。
最後に
今回は階層ありクラスタリングのウォード法について解説をしました。
考え方がシンプルなだけに汎用性が高く、バランスのよいクラスタリングを可能にする分析方法です。階層ありクラスタリングの中では頻繁に用いられるものなので、この記事を通して理解を深めていただければ幸いです!!
本格的にAIを学ぶならキカガク長期コース
本記事では、基礎的な内容について解説を行ないましたが、より本格的にAIを学んでみたいという方にはキカガク長期コースの受講をお薦めします。
- 基礎理論からAI搭載のWEBアプリ開発まで幅広く学習可能
- 将来追加されるものも含めて、プロによる全ての講義動画がずっと見放題
- 質問し放題のチャットや定期的な個別メンタリングなどのサポート体制
- IT専門のキャリアアドバイザーによる転職サポート
- 中央省庁からの給付金対象であるため受講料が最大70%
- ディープラーニングE資格の受験資格を獲得可能
興味はあるけど、いきなり受講を申し込むには抵抗があるという方は、キカガク長期コースの無料オンライン説明会も是非活用してみてください!!