今回は画像認識で用いられるニューラルネットワークである畳み込みニューラルネットワーク (CNN)を解説していこうと思います。
画像処理のために畳み込みとプーリングを導入したニューラルネットワーク
CNNは画像データの特徴を適切に処理するために考えられたニューラルネットワークです。従って、従来のニューラルネットワークとは異なる特徴があります。
(従来のニューラルネットワークを知らないという方は↓も是非お読みください)
ここでは、そもそもなぜCNNが必要になったのかという背景から始めて、CNNの考え方を初心者でも理解できるように説明していきたいと思います。
画像データとはどんなものか?
CNNの話をする前提として、そもそも画像データとはどんなものかをはっきりさせておきたいと思います。
例えば、以下のような犬の画像があるとします。

画像というの以下に示すように、小さな区画(ピクセル)の集合体です。各ピクセルが明るさなどの情報を持っており、それが組み合わさることで1枚の画像が形成されます。
(実際のピクセルはもっと細かいので、以下のピクセルは飽くまでイメージです)

また、カラー画像の色は色の三原色である赤・緑・青(RGB)がどのくらいの強度(明るさ)で組み合わされているのかで決まります。各ピクセル単位で色を持っているわけですから、各ピクセルにはRGBの3つチャンネルが存在します。
一例として、横に100個・縦に100個のピクセルが並んだカラー画像があれば、$100 × 100 × 3 = 30000$個のデータがあるということです。
なぜ新しいニューラルネットワークが必要なのか?
ここからはそもそもなぜ新しいニューラルネットワークが必要なのかを考えてみます。
従来のニューラルネットワーク(以下では、全結合層と呼びます)はシンプルに書けば以下のような構造でした。
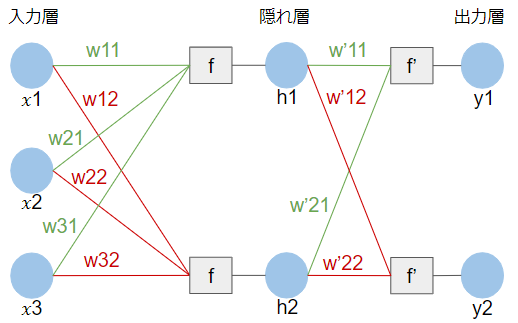
仮に30000個のデータを持つ画像を全結合層に入力するとすれば、1つのデータが入力層の1つのノードに対応することになるので、入力層のノードは30000個になります。
もちろん、このようなやり方も計算上は可能ですが、各ノードにデータがばらばらに入力された時点で、もともと画像として持っていた特徴を失ってしまうため、このようなやり方は適切とは言えません。
では、もともと画像として持っていた特徴というのはどういったものでしょうか?
画像には一般的に言って次のような特徴があります。
- 位置が近いピクセル同士は似たような値になる
- 位置が遠いピクセル同士の関連性は薄い
- RGBの各チャンネルには関連性がある
これらの特徴は直感的にも理解しやすいのではないかと思います。

例えば、画像中央の赤と青のピクセルは互いに隣接しており、どちらも犬の体の一部なので、互いに似たピクセルだと言えるでしょう。一方で、画面の右端にある黄色のセルは、赤や青のセルから離れた位置にあって、植物の一部なので、赤や青とは大きく異なるピクセルということになります。
また、RGBの組み合わせで色が決まるということを考えれば、これらの3つの間にも密接なつながりがあることは分かっていただけると思います。
ただ、残念なことに全結合層ではこのような画像ならではの特徴を生かすことはできません。繰り返しになりますが、入力層の各ノードにばらばらにデータを入れるしかなく、結果的に画像の特徴を生かせず、非効率なモデルとなってしまいます。
この背景を鑑みて、画像データを適切に処理するために考えられたのがCNNです。
CNNとは?
では、ここからCNNの中身に入っていきたいと思います。
先に言っておくと、CNNでも全結合層を使わないわけではありません。
例えば、画像の識別などでは、「この画像は犬だ」のように結論を出す必要があるので、最後は従来のニューラルネットワークである全結合層を使います。ただし、いきなり全結合層に入力するのではなく、その前に処理を施します。その処理がCNNの特徴です。
処理には「畳み込み」と「プーリング」の2種類があるので、それぞれ見ていきたいと思います。
畳み込み
畳み込みではフィルター(またはカーネルと呼ばれる)を使って、画像の特徴を抽出します。これはディープラーニングに限ったことではなく、画像処理で一般的に使われるテクニックです。
例えば、ある画像に特定のフィルターを適用することによって、以下のように画像の輪郭を抽出することもできます。

従来の画像処理では人間がフィルターを設計して、上記のように画像の特徴を抽出していました。しかし、ディープラーニングにおいては、このフィルターが学習の対象になります。つまり、画像が猫であるかどうかを判定するモデルであれば、猫の特徴を抽出できるようにフィルターを学習させることになります。
では、フィルターをもう少し具体的に見てみましょう。
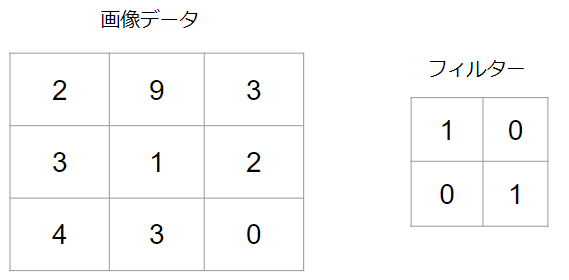
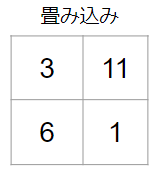
例えば、以下のような3×3のピクセルを持つ画像があるとします。数値はピクセルが持つデータの値です。そして、それに対して2×2のフィルターを適用してみます。
では、まず左上からフィルターを適用します。
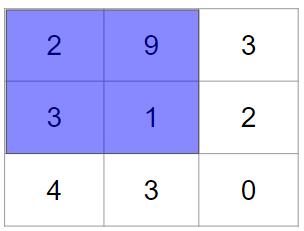
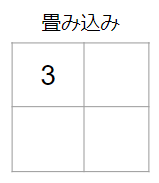
フィルターを適用する際には、画像のピクセルデータの値とフィルターの各値の積を求め、それらを足し合わせます。今回のケースですと、具体的には次のような計算をします。
$2 × 1 + 9 × 0 + 3 × 0 + 1 × 1 = 3$
では、次に右上にフィルターを適用します。
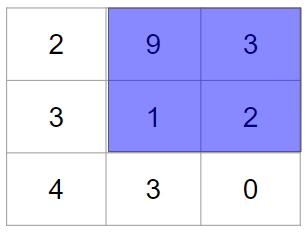
計算結果は、$9 × 1 + 3 × 0 + 1 × 0 + 2 × 1 = 11$です。
計算の流れが掴めてきたでしょうか?
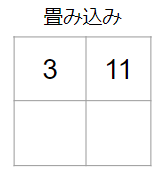
同様に左下と右下にフィルターを適用すると、畳み込み結果は以下の通りです。
これが畳み込みです。最初に例でも示したように、畳み込みによって画像の大局的な特徴を捉えることができます。
今回は簡単に説明するため、フィルターが1つでしたが、実際の場合にはフィルターが複数あり、それら全てを目的に合わせて最適化していくことになります。
以上が畳み込みの基本ですが、畳み込みを実行する際に使われるちょっとしたテクニックについても紹介しておきます。
ストライド(Stride)
ストライドとはフィルターを移動する間隔のことです。
上記の例では、フィルターを最初に左上に適応した後、そこから1ピクセルだけずらして、右上に適応していました。従って、stride=1の事例です。
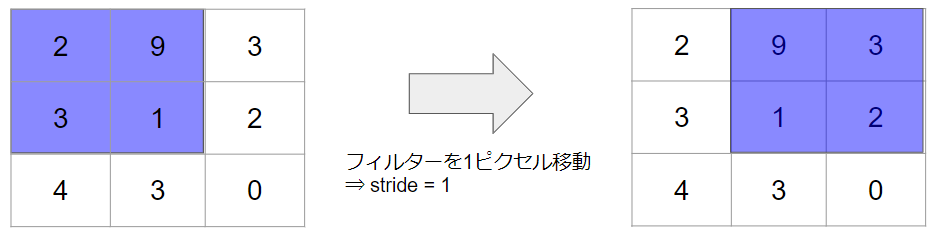
対象とする画像サイズが大きい場合などには、ストライドの値を大きくして、ピクセルを飛ばしながらフィルターを移動させることもあります。
パディング(Padding)
パティングとは画像の周囲に新たなピクセルを追加することです。
具体的に図示すると、次のような形になります。
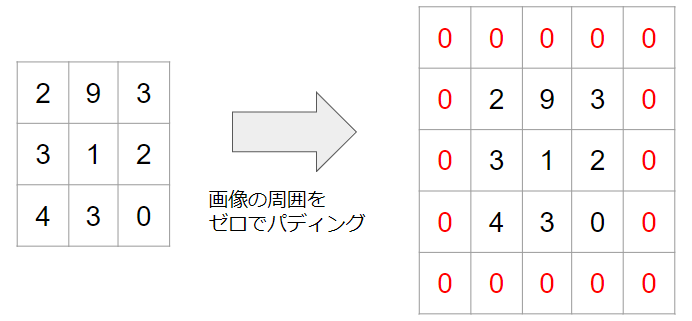
周囲に値がゼロのピクセルが追加されていることが分かると思います。
パディングの際には、ピクセルの値をゼロにすることが多く、そのような場合はゼロパディングと呼ばれます。
では、パディングには一体どのような効果があるのでしょうか?
1つには画像の端のピクセルに対しても平等にフィルターが適用されるようになることです。
パディングが無い場合には、以下のように、左右の列に対してはフィルターの適用回数が1回、中央の列にはフィルターの適用回数が2回とアンバランスです。
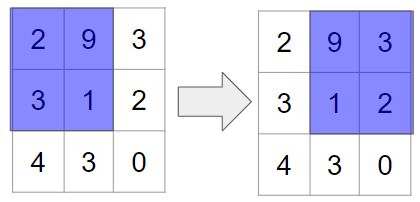
一方で、ゼロパディングを施すと、全ての列に対してフィルターが2回適用され平等になります。
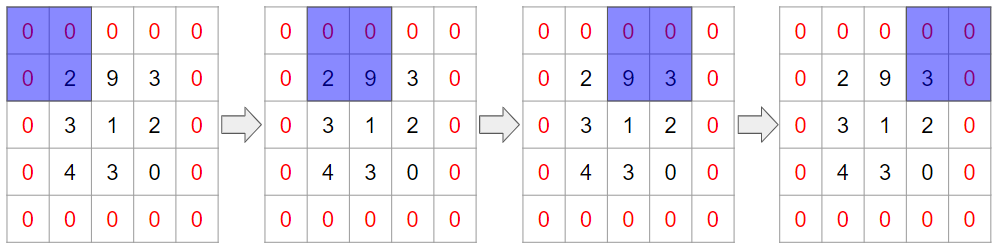
もう1つには、畳み込み後の画像サイズを調整できることです。これは上記の例を見ればお分かりいただけるかと思います。
パディング無しの場合にはフィルターを横へ動かす回数は2回ですが、パディング有りの場合は4回となっています。これは結果的に畳み込み後の画像サイズがパディングの有り・無しで変わることを意味しています。
ちなみに、パディングやストライドを踏まえた畳み込み後の画像サイズは以下の数式で表されることが知られています。
縦:$\frac{H + 2P_{h} – F_{h}}{S_{h}} + 1$
横:$\frac{W + 2P_{w} – F_{w}}{S_{w}} + 1$
入力画像の縦横サイズ:$(H, W)$
フィルターの縦横サイズ:$(F_{h}, F_{w}$)
ストライドの縦横幅:$(S_{h}, S_{w})$
パディングの縦横幅:$(P_{h}, P_{w})$
プーリング
プーリングとは情報を圧縮する行為です。
こちらは早速具体例を見てみましょう。例えば、畳み込みによって以下のような結果が得られているとします。
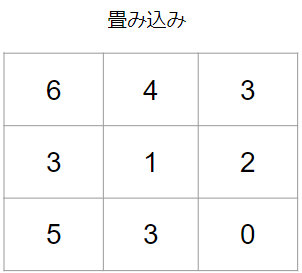
これに対してプーリングを行なってみたいと思います。プーリングはいくつか種類がありますが、今回は2×2のMAXプーリングをやってみます。
MAXプーリングは決められた範囲の最大値を取り出す操作で、今回は2×2なので、その範囲ごとに見ていきます。例えば、最初は次の範囲が対象です。
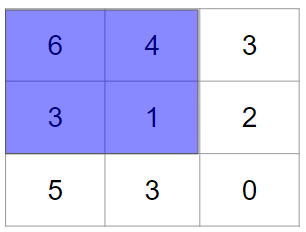
青色の領域の最大値を見つければよいので、答えは6です。
同様の操作を右上、左下、右下にも行なえば、プーリング結果は次のようになります。
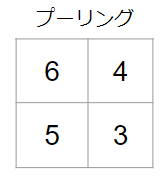
MAXプーリングの操作はこれで完了です。
ちなみに、平均値プーリングというのもあり、その場合には求める値が最大値ではなく平均値になります。
また、プーリングによって画像のサイズが変わることもお分かりいただけたかと思いますが、プーリング後の画像サイズは以下の数式によって計算可能です。結論を言うと、畳み込みの場合と同じ形の計算式になります。
縦:$\frac{H + 2P_{h} – F_{h}}{S_{h}} + 1$
横:$\frac{W + 2P_{w} – F_{w}}{S_{w}} + 1$
入力画像の縦横サイズ:$(H, W)$
フィルターの縦横サイズ:$(F_{h}, F_{w}$)
ストライドの縦横幅:$(S_{h}, S_{w})$
パディングの縦横幅:$(P_{h}, P_{w})$
操作自体は簡単だったと思いますが、プーリングはそもそも何のためにやっているでしょうか?
操作を見て分かるように、プーリングを行なうことで、いくつかのピクセルの情報が1つに圧縮されてしまいます。言い換えれば、画像情報の一部は捨てていることになります。
これは言い換えれば、画像の位置が数ピクセル程度ずれたくらいでは、モデルが出力する結果は変わらないと言うこともできます。つまり、画像の多少の変動や揺らぎがあっても、影響を受けないモデルになるということです。
ちょっと画像の位置が変わっただけで、結果がコロコロ変わってしまうモデルよりも、このようなモデルの方が堅牢でメリットがあると考えられています。
ちなみに、プーリングは最大値や平均値を取り出すだけの操作なので、特に学習とは関係はありません。
補足
今回は基礎を理解いただくため、畳み込みもプーリングも非常にシンプルな形で説明しましたが、実際のモデルではこれらの動作は複数回行なわれます。
畳み込みやプーリングで得られた結果を全結合層に入力して、最終結果を得るのが一般的な流れとなります。
以上が畳み込みニューラルネットワークの基礎的な説明となります。
本格的にAIを学ぶならキカガク長期コース
本記事では、基礎的な内容について解説を行ないましたが、より本格的にAIを学んでみたいという方にはキカガク長期コースの受講をお薦めします。
- 基礎理論からAI搭載のWEBアプリ開発まで幅広く学習可能
- 将来追加されるものも含めて、プロによる全ての講義動画がずっと見放題
- 質問し放題のチャットや定期的な個別メンタリングなどのサポート体制
- IT専門のキャリアアドバイザーによる転職サポート
- 中央省庁からの給付金対象であるため受講料が最大70%
- ディープラーニングE資格の受験資格を獲得可能
興味はあるけど、いきなり受講を申し込むには抵抗があるという方は、キカガク長期コースの無料オンライン説明会も是非活用してみてください!!













