今回は第1次AIブームで活躍した探索木というアルゴリズムを取り上げてみます。
※第1次AIブームについて知りたい方は↓をご覧ください。
探索木は突き詰めて言えば、スタートからゴールに向かって取り得る行動を全て列挙し、その中からゴールまでの最短ルートを見つけるというアルゴリズムです。
人工知能の計算力にものを言わせる力技のようなアルゴリズムですが、初めて耳にされた方にはピンと来ないかもしれないので、迷路の例を使って一歩一歩解説していきます。
全ての行動を洗い出す
さて、今回は以下の迷路において、どうやってゴールまで辿り着くかを探索木を使って考えてみます。
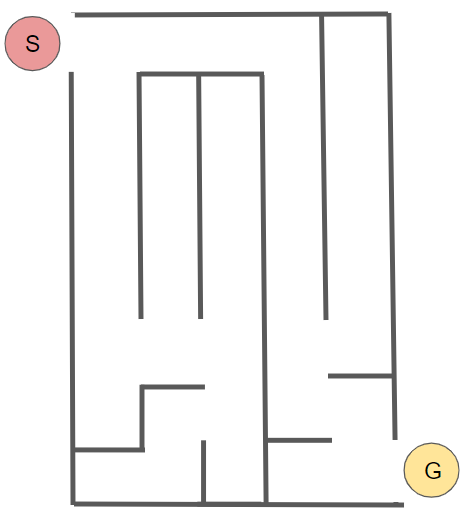
繰り返しになりますが、探索木というのはまず全ての行動を列挙するのでしたね。迷路においては、分岐点(複数のルートが選択可能な場面)が幾度も登場するので、分岐点に差し掛かる度に、選択可能なルートを漏れなく検討していきます。
実際に全ての選択可能なルートを記載すると、次のようになります。
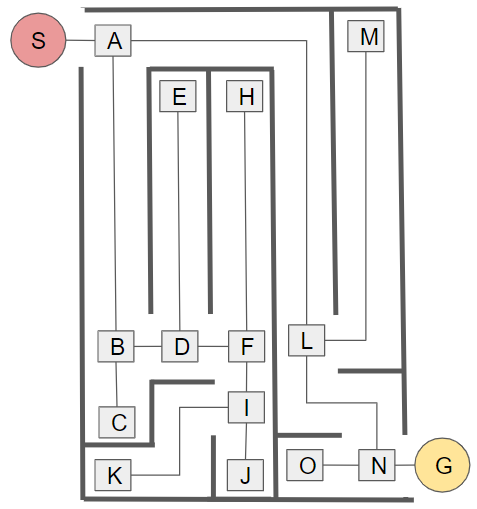
分岐点と行き止まりにアルファベットを1つずつ割り当てています。迷路全体を覆っているので、選択可能な全てのルートを網羅できていることが分かりますね。
次に迷路の枠を取り外し、スタート地点(S)を頂点に置く形で次のように図を書き換えます。見た目は変わっていますが、線のつながり方に変更はありません。
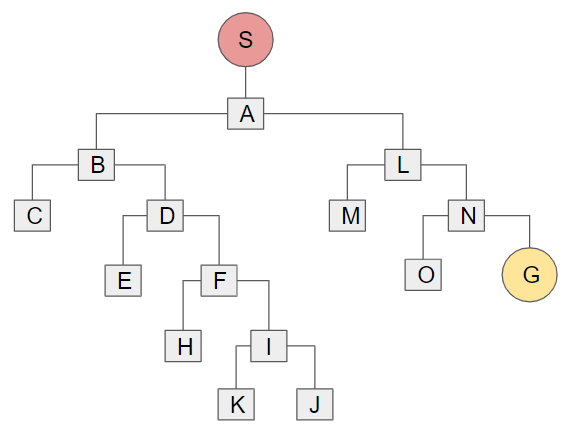
このような形に変形することで、選択しうるルートのパターンが見やすくなりましたね。このように、木の幹から枝が伸びていくような図で表せることから探索木という名前がつけられています。
ここまでで全ての行動を洗い出せたので、後はこの探索木を地道に調べていけばゴールまでのルートは導けそうです。ただし、探索木を調べる方法として幅優先探索と深さ優先探索の2種類があるので、次はこれらを説明したいと思います。
幅優先探索とは?
幅優先探索とは、出発点に近い点から順に探索木を調べていく探索方法です。今回の例に対して検索を行なう順番で番号を振ると、次のようになります。
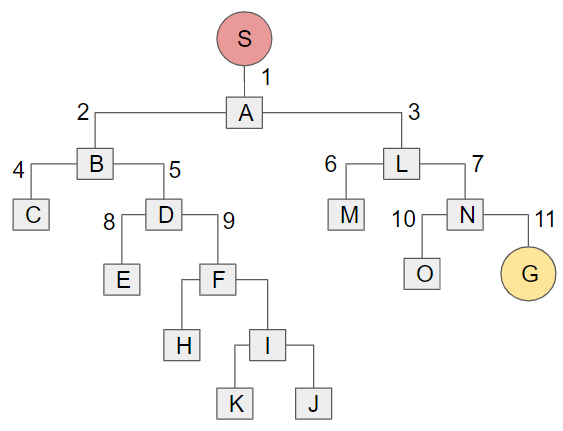
出発点に近い方から調べていくため、確実にゴールまでの最短ルートを発見することが可能です。一方で、途中のルートを記憶しておく必要があるため、メモリ(データを短期的に保持する場所)を大きく消費するという欠点があります。
どういうことかと言うと、上図から分かるように、A⇒Bというルートを調べたら、次はA⇒Lというルートを調べます。そして、その後でCに行くわけですが、その際に「A⇒B」という過程を記憶しておいて、「A⇒B⇒C」のようにつなげてあげなければなりません。「A⇒B」というルートを調べ終わったからと言って、「A⇒B」という情報を忘れてしまうと、Cに到達した時にどこから来たのか分からなくなってしまいます。これではルート探索の意味がなくなってしまうので、途中のルートをメモリに保持しておく必要があるということです。
〇 確実に最短ルートを発見することができる。
× 途中のルートの記憶が必要なため、メモリを消費しやすい
深さ優先探索とは?
深さ優先探索とは1つの経路を終わりまで調べてから次の経路を調べる探索方法です。 今回の例に対して検索を行なう順番で番号を振ると、次のようになります。
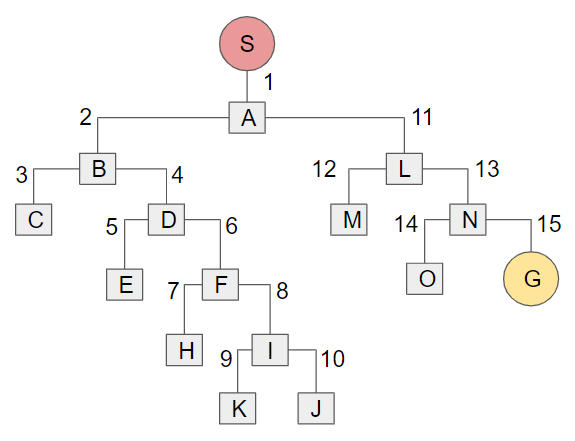
図を見れば幅優先探索との違いはご理解いただけるかと思います。この探索方法では1つ1つのルートを調べつくして次に行くので、幅優先探索のように途中のルートを記憶しておくという必要がありません。すなわち、メモリの消費が少なくてすむのです。一方で、ゴールまでのルートを発見したとしても、それが最短であるかどうかは分かりません。運よく一発で最短ルートに当たればよいですが、場合によっては全てのルートを探索し尽くすことになります。
〇 途中のルートを記憶しておく必要がないため、メモリ消費が少ない
× 最初に見つかった正解ルートが最短とは限らない
最後に
今回は迷路の例を用いて探索木の考え方を解説してみました。
一度分かってしまえば非常にシンプルな考え方ですが、第1次AIブームの火付け役となったアルゴリズムということで是非覚えておきたいですね!!
最後になりますが、より詳しくAIを学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!













