今回は単純パーセプトロンの限界をテーマにしてみようと思います。
単純パーセプトロンでは線形分離可能な問題しか解けない
単純パーセプトロンとは隠れ層(中間層)を持たない最もシンプルなニューラルネットワークのことです。つまり、非常にシンプルなニューラルネットワークでは解ける問題が限られているというのが今回取り上げる論点です。
「単純パーセプトロンとは?」については↓で説明しているので是非合わせてお読みください。
「線形分離可能」という言葉に馴染みが無い方もいると思うので、まずはこの言葉の意味を明確にし、なぜ単純パーセプトロンに限界があるのかを説明していきたいと思います。
線形分離可能とは?
線形分離可能の意味を理解するにあたって、二値分類問題を考えます。二値分類問題なので、何かしらのデータがある時にそれが2つのグループのどちらに属するのかを判定するということになります。具体例で言えば、あるメールの文面を見てスパムであるかないかを判定するといったようなものです。
二値分類というのはデータを2つのグループに分けるということですから、言い換えればデータの境界を定めるということになります。例えば、以下の図にある赤い点と青い点が異なるグループのデータだとして、図の黒線のように境界を決めればデータを分類することができます。なぜなら、境界の内側なら青のグループ、境界の外側なら赤のグループと即座に判定できるからです。
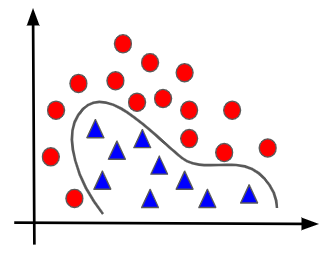
このように境界線を引く操作こそが分離です。そして、今回はその分離に「線形である」という条件がついています。
線形という言葉を聞いたときに皆さんは何を思い浮かべますか?
少し正確さに欠けた言い回しになってしまいますが、線形という言葉に対しては直線のイメージを持っていただくのが分かりやすいと思います。つまり、「線形分離可能」とはデータの境界を直線によって定めることができるという意味です。ちなみに、上図で示した境界線は明らかに直線ではありませんから、これは線形分離ができない例ということになります。線形分離可能とは図で言うと、以下のような状態です。
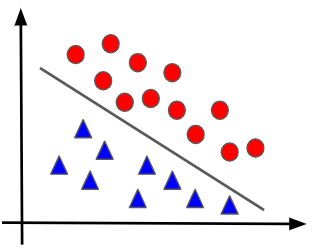
ここまでで「線形分離可能」のイメージは掴んでいただけたでしょうか?
考え方はこれで十分なのですが、ここからは少し数式も交えて「線形分離可能」を説明してみたいと思います。まずは簡単のためにデータは1次元、つまり二値分類に使える指標が1つしかないという設定で考えます。例えば、ウエストのサイズだけ(1つの指標)から肥満であるかないかを判定するといったようタスクです。
1次元において線形分離可能であるとは数学的には次のような定義となります。
異なる2つのデータのグループAとBがある。Aに属する全てのデータ$x_{A}$に対しては常に$wx_{A}+b > 0$、Bに属する全てのデータ$x_{B}$に対しては常に$wx_{B}+b < 0$が成立するような$w,b$を求めることができる。
若干ややこしい言い回しですが、まず$wx+b$というのは、よく知られているように直線を表す式です。つまり、上記の説明は、グループAのデータに対しては正、グループBのデータに対しては負となるような直線が存在するということです。まさに先ほど説明した2つのグループの境界を直線によって求められるというのと同じ話です。これを任意のN次元に拡張すると、次のように書き直すことができます。
異なる2つのデータのグループAとBがある。Aに属する全てのN次元データ$x_{A}$に対しては常に$w_{1}x_{A_{1}}+w_{2}x_{A_{2}}+…+w_{N-1}x_{A_{N-1}}+w_{N}x_{A_{N}}+b > 0$、Bに属する全てのN次元データ$x_{B}$に対しては常に$w_{1}x_{B_{1}}+w_{2}x_{B_{2}}+…+w_{N-1}x_{B_{N-1}}+w_{N}x_{B_{N}}+b < 0$が成立するような$w,b$を求めることができる。
係数$w$や変数$x$はN個に増えていますが、1次式の正負でデータを分類できるという点は先ほどと同様です。
以上が線分離可能の説明となります。
単純パーセプトロンの限界
では、線形分離可能の定義を理解したところで、次は線形分離と単純パーセプトロンの関係性を確認してみましょう。
ちなみに「単純パーセプトロンとは?」に関しては、↓の記事で説明していますので、忘れてしまったという方は是非読んでみて下さい。
単純パーセプトロンは入力層と出力層のみ(隠れ層なし)なので、出力$y$は次のように表すことができます。ここでは入力は仮に3次元だとします。
$y = w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b$
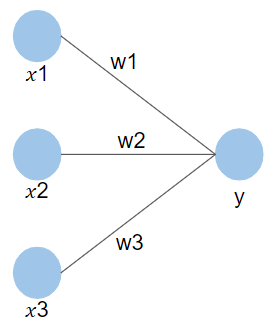
変数$x$が3つありますが、出力が$x$の1次式で表せるので、$y$の値の正負でデータの境界を決めれば線形分離をしていることになります。裏を返せば、この数式の特性上、単純パーセプトロンは線形分離可能な分類問題しか扱えないという結論になります。
これが単純パーセプトロンの限界です。分類問題において、直線的ではない複雑な境界を求めるためには単純パーセプトロンでは不十分であるということが分かります。
最後に
今回は単純パーセプトロンの限界について基礎から解説してみました。
線形分離可能のイメージを即座に理解するのが難しいかもしれませんが、慣れてしまえば難しいものではないので、是非何度も記事を読み返してみて下さい!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも活用してみてください!













