今回はニューラルネットワークがどのように学習を行うのかをテーマにしてみたいと思います。
- ニューラルネットワークの順伝播を計算する
- 順伝播の結果と正解データを用いて損失関数を計算する
- 損失関数から誤差逆伝搬でパラメータの勾配を計算する
- 勾配を用いてパラメータを更新する
これがざっくりとしたニューラルネットワークの学習の流れです。
この流れが理解できるようになれば、ニューラルネットワークの全体像が見えてきて学ぶのが楽しくなってくるのではないかと思います。
とはいえ、これだけでは知らない言葉があって理解できないという方もいると思うので、1つ1つのステップの概要を詳細に立ち入り過ぎないで平易に解説してみたいと思います。
なお、ニューラルネットワークの基礎に自信のない方は『【まずはざっくり理解しよう】ニューラルネットワークの概要を分かりやすく解説』も是非一緒に読んでみて下さい。
①ニューラルネットワークの順伝播を計算する
まず順伝播というのはニューラルネットワークの入力層から出力層に向かって順に計算していくことです。
例えば、次の図1のようなニューラルネットワークがあるとします。
(※簡単のためにバイアスは考えないものとします)
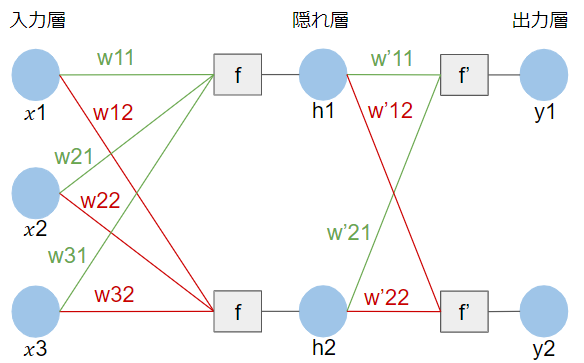
順伝播では入力層から出力層に向かって随時計算をしていくので、結果的には次のような計算を行うことになります。
- $h_{1} = f(w_{11}x_{1} + w_{21}x_{2} + w_{31}x_{3})$
- $h_{2} = f(w_{12}x_{1} + w_{22}x_{2} + w_{32}x_{3})$
- $y_{1} = f^{\prime}(w^{\prime}_{11}h_{1} + w^{\prime}_{21}h_{2})$
- $y_{2} = f^{\prime}(w^{\prime}_{12}h_{1} + w^{\prime}_{22}h_{2})$
この計算過程については『【まずはざっくり理解しよう】ニューラルネットワークの概要を分かりやすく解説』でも解説していますので、上記の計算がピンと来ないという方は是非併せてご覧ください。
出力層の計算結果は言い換えればニューラルネットワークが導き出した結果なので、次のステップ以降で学習のために、この結果を利用します。
②順伝播の結果と正解データを用いて損失関数を計算する
このステップの中身を説明する前に、大前提として、ニューラルネットワークに学習をさせるとは詰まるところ何を意味するのでしょうか?
私たちはニューラルネットワークを用いて、例えば未知のデータの分類をしたり、将来のことを予測したりしたわけですが、一切学習をしていないニューラルネットワークに入力を渡したとしても、出力される結果は適当な値なので全く信用することができません。これを信頼に足る値にするために、ニューラルネットワークの学習が必要になります。
では具体的に何をするのかと言えば、まず学習においては正解が分かっているデータを準備します。例えば、直近1週間分の株価の値動きから翌日の株価を予測するニューラルネットワークを作りたいのであれば、学習時には「直近1週間の株価」と「その翌日の株価」をセットで用意します。
とりあえずニューラルネットワークを組んで、それに「直近1週間の株価」を入力すれば、何らかの出力値を返しますが、これが正解(翌日の株価)に近しい値でなければ意味がありません。そこで、学習時には正解が分かっているわけですから、ニューラルネットワークの出力と正解データのずれを計算します。当然ながら、このずれが小さい方が性能の良いニューラルネットワークということになります。後ほど改めて説明をしますが、このずれが小さくなるようにニューラルネットワークを矯正していくことをニューラルネットワークの学習と呼んでいます。
損失関数はまさにニューラルネットワークの出力と正解データのずれを表現するのに使われる指標です。損失関数を計算することによって、ニューラルネットワークがどのくらいに正解に近い値を出力できているのかを評価することができます。
損失関数の一例としては、次の二乗和誤差があります。()の中が正解データとニューラルネットワークの出力値の差なので、損失関数の値が小さいことはニューラルネットワークが正解に近い値を出力していることを意味します。
$E = \frac{1}{2}\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}$
$y_{i}:i番目の出力層の値$
$\hat{y_{i}}:i番目の正解データ$
損失関数は他にも有名なものがありますが、その詳細はまた別の機会に改めて紹介したいと思います。
③損失関数から誤差逆伝搬でパラメータの勾配を計算する
繰り返しになりますが、損失関数を用いることによってニューラルネットワークの出力の精度を評価できるようになりました。ただし、学習の目的は出力が正解に近づくようにニューラルネットワークを改善していくことなので、評価結果をニューラルネットワークに反映しなければなりません。このステップではその反映方法を考えてみます。
そもそもニューラルネットワークの出力値というのは何によって決まってくるのでしょうか?先ほどの図1のニューラルネットワークの順伝播の計算を見ると、結局重み$w$の値次第であることが分かると思います。ニューラルネットワークの構造を一旦定めてしまえば、計算方法は常に一定なので、出力結果を変更したければ重み$w$の値を変える必要があります。
もちろん$w$を変更すると言っても、適当にやれば、反って出力値と正解データのずれが大きくなってしまう恐れがあるので、$w$を変更したら出力値がどう変更されるのかをちゃんと把握したうえで、$w$を動かさなければなりません。
では、$w$を動かした時に出力値がどう動くのかは何をすれば分かるでしょうか?答えは数学の微分計算です。数学で微分は$\frac{\partial y}{\partial x}$などと表記しますが、これが意味するところは「$x$を少し増加させると$y$はどのように変化するのか」ということです。例えば、これが正の値であれば$x$を少し増やせば$y$も増えるということですし、逆に負の値であれば$x$を少し増やせば$y$は減るということです。
私たちは損失関数の値をできるだけい小さい方向に持っていきたいので、損失関数を重みで微分することによって、損失関数を小さくするためには$w$を増やせばよい、または減らせばよいというのを掴むわけです。このような損失関数の重みによる微分値のことを勾配と呼び、ニューラルネットワークの学習において非常に重要役割を担っています。
というわけで、図1の例であれば重み$w$が10個あるため、$\frac{\partial E}{\partial w}$を10通り求めればよいということになりますが、ここで少し計算の仕方について説明してみたいと思います。
例えば、入力層から隠れ層にかけての$w_{11}$による微分である$\frac{\partial E}{\partial w_{11}}$を求めることを考えます。(ここでは微分の細かい計算は割愛しますが)順伝播の数式を見れば分かるように、入力層から損失関数を求めるにいたるまで何重にも計算を繰り返すことになるため、$\frac{\partial E}{\partial w_{11}}$を一気に求めるのは実は結構大変な計算になります。図1の例では隠れ層が1つだけなのでまだよいのですが、実際には何百何千と隠れ層が存在するため、一気に計算するのは計算コストがかなり高くなってしまいます。
そのため、実際には微分の便利な性質を使って、一気に計算をしなくても済むように工夫をしています。その便利な性質と言うのが微分の連鎖律です。
$\frac{\partial z}{\partial x} = \frac{\partial z}{\partial y} \frac{\partial y}{\partial x}$
イメージとしては$z$と$x$の間に$y$を噛ませることができるということですね。仮に$p = w_{11}x_{1} + w_{21}x_{2} + w_{31}x_{3}$とすれば、この連鎖律を使って以下のような式変形ができることになります。
$\frac{\partial E}{\partial w_{11}} = \frac{\partial E}{\partial p} \frac{\partial p}{\partial w_{11}}$
先ほども言ったように損失関数は入力層から見て、何重にも計算を繰り返した後なので、$\frac{\partial E}{\partial w_{11}}$を求めるのが大変そうですが、それに比べて$\frac{\partial p}{\partial w_{11}}$であればシンプルに計算できそうです。では、$\frac{\partial E}{\partial p}$の方はどうするのかと言うと、ここも微分の連鎖律を適用して計算しやすい形に書き換えていきます。
このような作業を繰り返していくと、一気に計算できないような複雑な微分計算が簡単な微分計算の和や積の形に書き換わってしまうのです。実際の計算においてもこの手法が用いられており、損失の関数の誤差が積や和の形で伝わっていく様子から誤差逆伝搬と呼ばれます。順伝播は入力層から始まりますが、逆伝搬は損失関数から始まるので、まさに逆になっていることがお分かりいただけると思います。
④勾配を用いてパラメータを更新する
誤差逆伝搬によって勾配が求まってしまえば、あとはその勾配を使って、重み$w$の値を更新するだけです。
$w_{new} = w_{old} ~ – ~ η\frac{\partial E}{\partial w}$
勾配の前に着く符号がマイナスになっているのは損失関数の値を小さくする方向に$w$を動かしたいからです。先ほども言ったように、仮に$\frac{\partial E}{\partial w}$が正であれば$w$を増やしたら$E$も増えるということなので、$E$を減らすには$w$を減らさなければなりません。逆に負であれば、$w$が増えると$E$が減るということなので、$w$を増やさなければなりません。こう考えれば、勾配の前にマイナスがついていることも納得いただけると思います。
ちなみに、勾配に掛かっている$η$は学習率と呼ばれるハイパーパラメータ(人間が予め決めておく数値)です。$η$が大きければ$w$は大きい幅で更新され、$η$が小さければ$w$は少しづつ更新されていくことになります。
そして、更新された$w$を使って再度順伝播を計算し、損失関数の値を求め、また$w$を更新するというのを繰り返していきます。
このようにしてニューラルネットワークは正解に近い値を出力できるように学習をしていきます。
最後に
今回はニューラルネットワークの学習の仕組みを非常にざっくり解説してみました。
今回はシンプルに概要をつかんでいただくため、本当に触りの部分だけの記述なので、より詳しい内容は今後どんどん追加していきたいと思います!!
最後になりますが、より詳しく学んでみたいという方は、AIの基礎からAI搭載WEBアプリ開発まで学べるキカガク長期コースも是非活用してみてください!