今回はディープラーニングにおいて有名な勾配消失問題とその対策となる活性化関数をまとめて取り上げていきたいと思います。
ニューラルネットワークの層が深くなると、誤差逆伝搬による学習が進まなくなる現象
誤差逆伝搬の概要は【流れを理解しよう】ニューラルネットワークの学習の仕組みをシンプルに解説で述べたた通りですが、ニューラルネットワークの層数が増えると、この仕組みがうまく機能しなくなるということです。
ニューラルネットワークの学習が進まないということは、どんなに頑張っても期待した出力を得られないことになってしまうので大問題ですね。
この問題は活性化関数とも大いに関係しているので、今回はその大問題の仕組みと対策を活性化関数の観点からできるだけ分かりやすく説明してみようと思います。
もし勾配や誤差逆伝搬などを忘れてしまった・分からないという方は是非↓の記事を読んでから本記事を読み進めてみて下さい。
勾配消失問題とは?
そもそも勾配というのは、損失関数をニューラルネットワークのパラメータ(重み)で微分したものでした。
勾配消失問題というからには、まさにその勾配が消えてほぼゼロになってしまうことが問題になっているわけです。では、なぜ勾配がほぼゼロになるとまずいのでしょうか?
$w_{new} = w_{old} ~ – ~ η \frac{\partial E}{\partial w}$
ニューラルネットワークは上記の数式によって重みが何度も更新されることによって、学習が進み、完成度を上げていく仕組みでした。勾配がほぼゼロだということは第2項の微分がほぼゼロになるので、重みがほとんど更新されなくなることを意味します。すなわち、学習が進まず、ニューラルネットワークの完成度が上がらないということです。
ここまでで「勾配がほぼゼロになるとまずい」ということはご理解いただけたと思いますが、そもそもなぜ勾配がほぼゼロになるという事態が発生してしまうのでしょうか?
その原因は活性化関数にあります。勾配は損失関数を重みで微分して求めますが、実際に損失関数を直接的に重みで微分するのは難しいので、微分の連鎖律という性質を使って、複数の微分を掛け合わせて求めるのでした。
$\frac{\partial X}{\partial Y} = \frac{\partial X}{\partial Z}\frac{\partial Z}{\partial Y}$
ニューラルネットワークの順伝播では活性化関数による計算があるので、誤差逆伝搬で遡っていく際には活性化関数の微分も発生します。従来のニューラルネットワークで活性化関数としてよく使われていたのは、【かみ砕いて説明します】ロジスティック回帰分析を分かりやすく解説で紹介したシグモイド関数でした。
細かい計算は省略しますが、シグモイド関数の微分値は必ず1より小さくなるという性質を持ちます。ニューラルネットワークの層が深い場合には活性化関数の計算が何度も発生するので、誤差逆伝搬において、その微分値を掛け合わせる回数も必然的に多くなります。
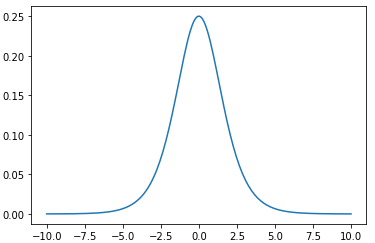
当然のことながら1より小さい値を何度も何度も掛け合わせれば、その値はどんどん小さくなっていき、最終的にはほぼゼロになってしまいます。このようにして、層が深いニューラルネットワークは勾配消失問題に直面することになります。
勾配消失問題を起こさない活性化関数
ここまでで、シグモイド関数の特性によって勾配消失問題が生じていることをご理解いただけたと思うので、活性化関数を変えることを考えます。
「活性化関数を変えてしまってもよいのか?」という疑問もあるかもしれませんが、そもそもシグモイド関数を用いていた理由は確率を表現するのに便利だからでした。シグモイド関数は必ず0~1の値を返すので、それを確率と解釈できるわけですね。ただ、最終的な結果を返す出力層いおいては確かに必要な性質ですが、途中の隠れ層においては必須と言うわけではありません。つまり、隠れ層の活性化関数には選択の自由があるわけです。
では、ここからシグモイド関数以外の活性化関数を紹介してみます。
tanh関数
読み方はハイパボリックタンジェント関数です。
$tanh(x) = \frac{e^x ~ – ~ e^{-x}}{e^x ~ + ~ e^{-x}}$
数式は一見すると複雑ですが、グラフはきれいな形をしており、-1~1までの値を取ることが分かります。従って、シグモイド関数のように確率を表すのには使えません。
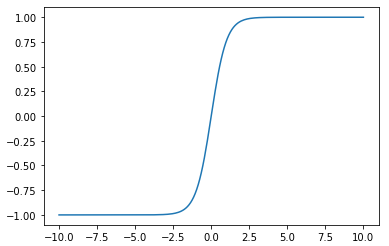
では、肝心の微分はどうでしょうか?
微分はグラフから分かるように最大値が1となっています。ということは、微分が確実に1より小さくなるシグモイド関数に比べて勾配消失問題を起こしにくいということができます。
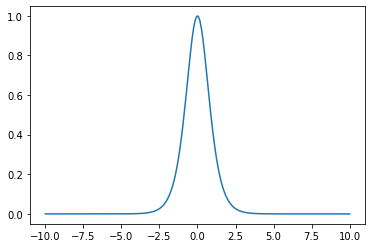
ただし、最大値は1であっても、ほとんどの場合で微分値が1より小さいので、勾配消失問題を完全に防げているわけではありません。
ReLU関数
読み方はレル関数です。
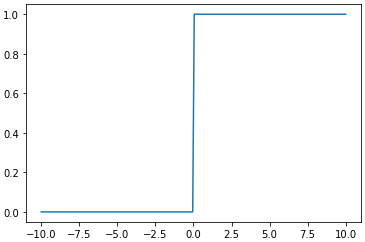
$y = max(0,x)$
maxというのは「大きい方を取る」という意味なので、xが0以下の場合はyは0、xがより大きければ、yはそのままxの値を取ることになります。
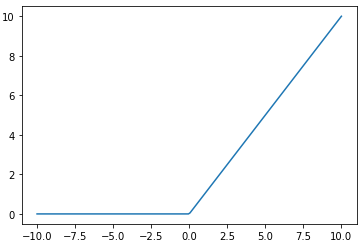
微分はxが正の領域では、必ず1になるため勾配消失が起こらないようになっています。実際に現在のニューラルネットワークでも多数用いられている実績があり、メジャーな活性化関数だといえます。ただし、xが負の領域では微分値が0になってしまうため、xが正の時しか使えない事には注意が必要です。
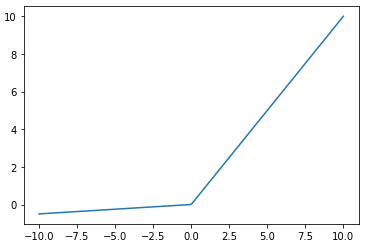
ちなみに、ReLU関数の派生版として以下のようなものが使われています。どれもReLU関数の改良を試みたものですが、実際にReLU関数よりもよい結果を出せるかどうかはケースバイケースになっています。
- Leaky ReLU:$x < 0$でもある一定の傾きを持つ
- Parametric ReLU:$x \geqq 0$ での傾きを1以外にする
- Randomized ReLU:$x \geqq 0$ での傾きをランダムに選択する
最後に
今回はニューラルネットワークでよく知られている勾配消失問題をその原因である活性化関数とともに解説してみました。
勾配消失問題はディープラーニングの話では頻繁に登場するので、是非本記事を読んで、基本を押さえていただければと思います!!
本格的にAIを学ぶならキカガク長期コース
本記事では、基礎的な内容について解説を行ないましたが、より本格的にAIを学んでみたいという方にはキカガク長期コースの受講をお薦めします。
- 基礎理論からAI搭載のWEBアプリ開発まで幅広く学習可能
- 将来追加されるものも含めて、プロによる全ての講義動画がずっと見放題
- 質問し放題のチャットや定期的な個別メンタリングなどのサポート体制
- IT専門のキャリアアドバイザーによる転職サポート
- 中央省庁からの給付金対象であるため受講料が最大70%
- ディープラーニングE資格の受験資格を獲得可能
興味はあるけど、いきなり受講を申し込むには抵抗があるという方は、キカガク長期コースの無料オンライン説明会も是非活用してみてください!!












