今回はディープラーニングの学習において欠かせない勾配降下法について解説してみたいと思います。
損失関数をニューラルネットワークのパラメータで微分することで勾配を計算し、その勾配を用いて損失関数が最小化する方向へパラメータを変化させていく最適化手法
損失関数というのはニューラルネットワークの出力値と正解データのずれを表すものです。そして、ニューラルネットワークの学習では、この損失関数を最小化することが目的です。そして、損失関数をパラメータで微分した勾配を用いて最小化を行うのが勾配降下法です。もし、この辺りの基礎的な内容に自信のない方は是非↓の記事から始めてみて下さい。
今回はその勾配降下法の問題点や改善方法をできるだけ分かりやすく解説してみたいと思います。
勾配降下法の問題
問題点の話に入る前に勾配降下法のイメージを確認しておきます。
勾配降下法によるパラメータの更新は次の式で表すことが可能です。
$w_{new} = w_{old} \quad – \quad η \times \frac{\partial E}{\partial w}$
$E$:損失関数
$w$:重みなどのパラーメータ
$η$:学習率
この数式はパラーメータの値を損失関数が小さくなる方向へ変化させるということを意味しているのでした。それを簡単な図で表現してみると次のようになります。
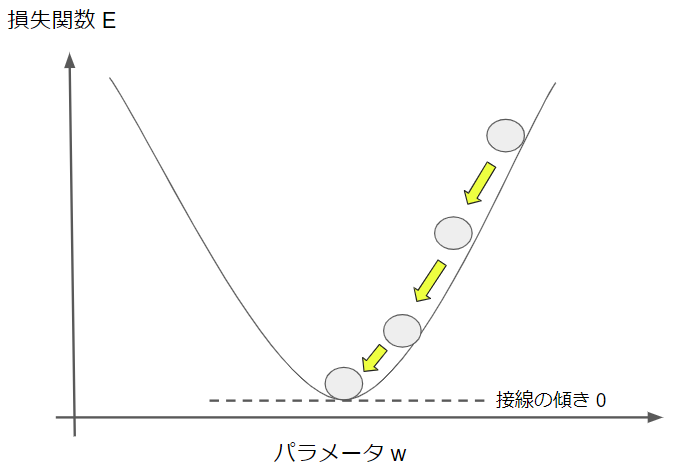
右上の●がスタート地点で、損失関数の値が大きい状態です。そこから勾配降下法によって、損失関数が減る方向にパラメータを徐々に更新していき、損失関数の最小値に辿り着いたらゴールです。
ゴール地点では損失関数をパラメータで微分した値はゼロになります。少し数学的な話になりますが、微分値とはそもそも接線の傾きを意味しており、図から分かるように損失関数の最小点での接線の傾きはゼロだからです。
これが勾配降下法によって損失関数を最小化する基本的な流れです。
では、ここからその勾配降下法の問題点を指摘してみたいと思います。
問題① 局所最適解に陥ることがある
先ほどの勾配降下法の例では損失関数のグラフが非常にシンプルでしたが、今回はもう少し複雑なものを考えてみましょう。
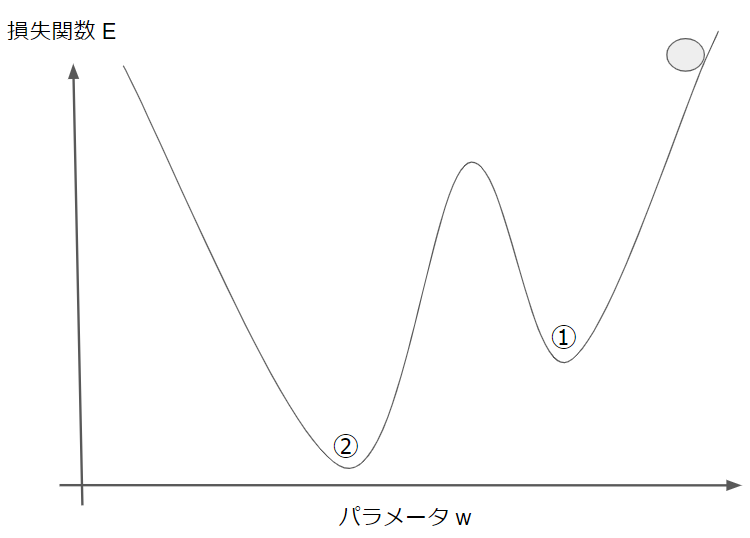
先ほどと同様に右上からスタートするとします。目的は損失関数を最小にすることなので、ゴールは②の地点です。
しかし、勾配降下法で少しづつパラメータを更新していくと①の地点で終了してしまう可能性があります。なぜなら、①の地点でも接線の傾きはゼロなので、パラメータの更新が止まるからです。
①のような地点を局所最適解、②のような真の最適解を大域最適解と言います。勾配降下法では両者の区別をつけることができないので、大域最適解ではなく、局所最適解で学習を終了してしまうことがあります。
ちなみに、パラメータが多次元になるとさらに厄介なことが起こります。以下の図はパラメータが$X,Y$の2つある場合ですが、赤い丸の点はXに関しては極小値ですが、Yに関しては極大値です。このような点は鞍点(あんてん)と呼ばれており、鞍点付近に落ち着いてしまうと抜け出すのは困難になります。
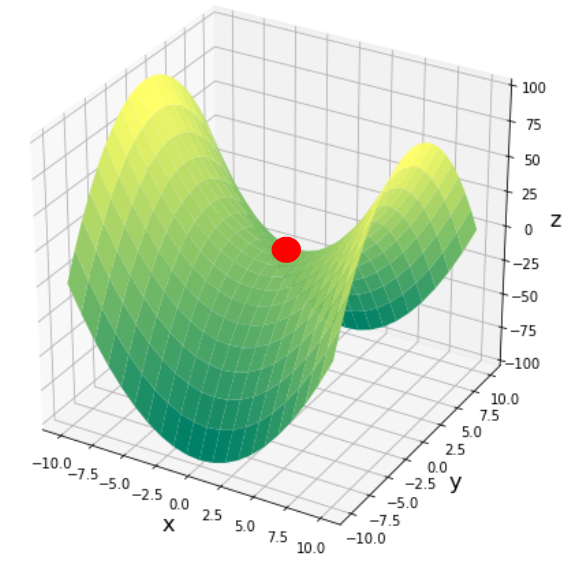
問題② 最適解に辿り着くのに時間がかかる
パラメータの更新量は微分値にも依存しますが、同時に学習率にも依存します。学習率は人間が自分で設定するパラメータで、予め大きな値に設定しておけば、パラメータの更新量もそれに合わせて大きくなります。
では、学習率を大きく設定し過ぎるとどのようなことが起こるでしょうか?
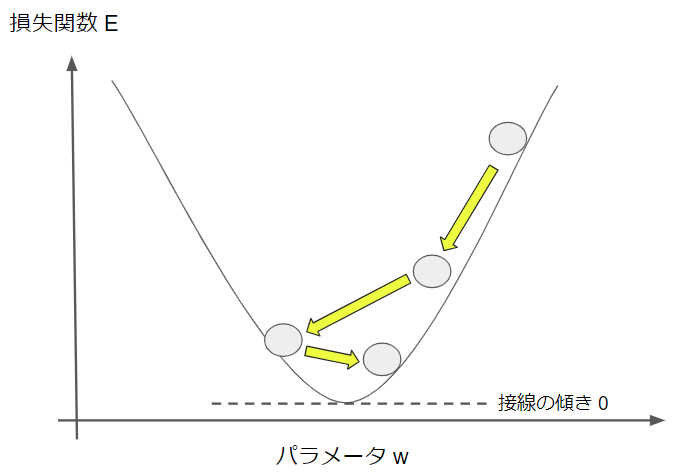
少し極端に図示していますが、学習率が大き過ぎると、更新量が大きいために最小点を通り越して、また戻ってくるような動きをします。最小点の周りを何往復もすることになってしまうので、これでは時間の無駄になってしまいますね。
では、これを避けるために学習率を小さく設定しておけばいいのでしょうか?
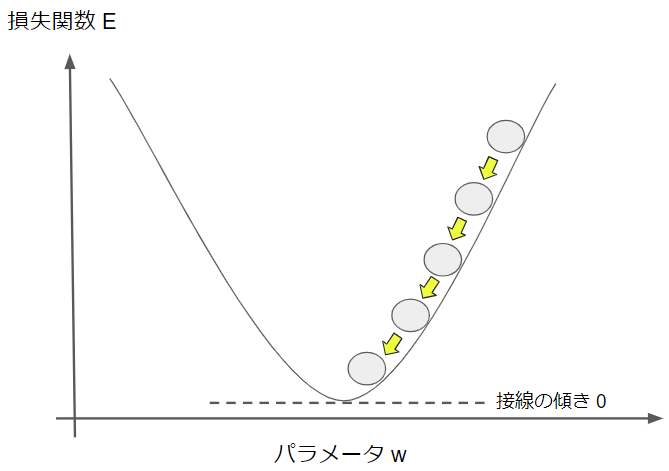
学習率を小さくし過ぎると、更新量が小さくなってしまい、なかなか学習が進まなくなります。そうすると、結果的に最小点に辿り着くのに時間がかかってしまうので、これもやはりいいとは言えません。
このように学習率の設定は難しく、適切な値にしないと学習が思ったように進まなくなります。
以上が勾配降下法の主な問題点として知られています。
勾配降下法の改善
ここからは今しがた紹介した勾配降下法の問題点を補うべく考えられたパラメータ更新の方法をいくつか紹介したいと思います。
確率的勾配降下法(SGD)
名前から分かるようにSGDは勾配降下法ととてもよく似ており、パラメータ更新の数式は全く同じです。違いは「確率的」というところなので、ここを説明してみたいと思います。
例えば、1000個の学習用データがあった場合に、勾配降下法では1000個のデータを使って損失関数を計算し、パラメータの更新量を求めます。これに対して、SGDでは全てのデータをまとめて使わず、例えば100個をランダムに抽出してパラメータの更新量を求めます。
100個をランダムに抽出する場合、それを10回繰り返すことになりますが、当然毎回損失関数が異なるので、パラメータの更新量や更新の方向もランダムになります。
このようにパラメータの更新に確率的な要素を取り入れたのがSGDです。こうすることで、ある時に局所最適解に落ち着いてしまったとしても、次の学習では損失関数が変わっているので、損失関数の微分値がゼロにならず、パラメータの更新が継続されます。
SGDでは、このようにして局所最適解に陥ってしまうことを回避します。
モメンタム
モメンタムのパラメータ更新式は次の通りです。勾配降下法に比べて少し複雑ですね。
$v_{new} = -η\frac{\partial E}{\partial w} |_{w_{old}} + αv_{old} \quad$
$w_{new} = w_{old} \quad + \quad v_{new}$
新しい変数として$v$が登場しています。$v_{old}$は前回のパラメータ更新量で、それを勾配に足して、今回のパラメータ更新量を求めています。
前回のパラメータ更新量を勾配に足すとどのような効果があるのでしょうか?
例えば、前回の更新量が正で、勾配も正である場合には、今回の更新量は勾配によって増加されます。一方で、前回の更新量が正で、勾配が負である場合には、今回の更新量は勾配によって減少されます。
これはよく坂道を転がるボールの運動に例えられます。以下の図に青矢印がボールの進行方向を表しますが、勾配によってボールが加速・減速される様子と似ています。ちなみに、モメンタムは「運動量」という意味なので、まさに物理的な運動に由来した命名になっています。
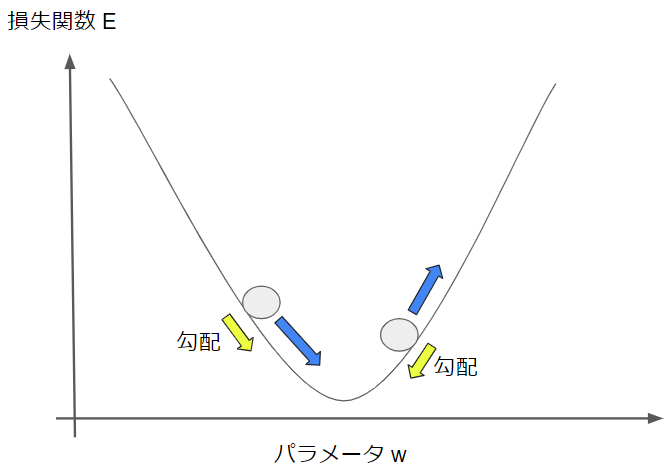
勾配だけで更新量を決めてしまうと、パラメータを更新する方向が急激に変化して、結果的に効率が悪くなることが知られており、これがSGDの欠点でもありました。モメンタムでは勾配(運動では加速度)と前回のパラメータ更新量(運動では速度)の両方を使うことで、安定して最適解に収束することができます。
AdaGrad
AdaGradのパラメータ更新式は次の通りです。
$h_{new} = h_{old} + (\frac{\partial E}{\partial w}| _{w_{old}})^2$
$η_{new}=\frac{η_{0}}{\sqrt{h_{new}}}$
$w_{new} = w_{old} \quad – \quad η_{new}\frac{\partial E}{\partial w}|_{w_{old}}$
$η_{0}$:学習率の初期値
まず第1式の$h$は過去の勾配を二乗和です。そして、$h$で学習率の初期値$η_{0}$を除算しています。つまり、学習率は学習が進むにつれて小さくなっていくということです。
しかも、勾配が大きければ大きいほど、学習率が小さくなっていくのが早まります。
勾配が大きいということはパラーメータの更新量が多いということですから、最初のうちにパラメータが大きく更新された場合は、後々で学習率が小さくなって、パラメータの更新が小幅になるということです。
このような仕組みを取り入れることによって、パラメータの更新量を調整するのがAdaGradの特徴です。
しかし、勾配の大小に関わらず、学習の回数(=イテレーション)が大きくなっていくと、学習率が小さくなり、学習が進まなくなってしまうのがAdaGradの課題です。
RMSProp
RMSPropはAdaGradの改良版で以下のような数式で表されます。
$h_{new} = αh_{old} + (1-α)(\frac{\partial E}{\partial w}| _{w_{old}})^2$
$η_{new}=\frac{η_{0}}{\sqrt{h_{new}}}$
$w_{new} = w_{old} \quad – \quad η_{new}\frac{\partial E}{\partial w}|_{w_{old}}$
$η_{0}$:学習率の初期値
$α$:定数
第1式で定数$α$を導入しています。過去の勾配の二乗和(第2項)に今回の勾配の値(第1項)をただ足し合わせるのではなく、$α$の大きさを調整することで、足し合わせる比率を調整ることができます。例えば、$α$を小さく設定しておけば、過去の勾配の二乗和の影響を小さくすることができます。
AdaGradでは過去の勾配の二乗和をそのまま利用していたので、学習率が小さくなってしまいました。それを回避するために、RMSPropでは過去の勾配の二乗和の影響を弱める工夫をしています。
Adam
Adamは数式は複雑であるため省略しますが、一言で言えば、モメンタムとRMSPropの組み合わせです。
モメンタムはパラメータ更新に勾配と前回の更新量の両方を用いる工夫を行ない、RMSPropは学習率の設定に過去の勾配の二乗和を考慮するという工夫をしたものでした。
その両方を取り入れたのがAdamで、パラメータの更新手法としてはかなり汎用的に使われています。
最後に
今回は勾配降下法の問題点とその改善について説明してみました。
これらを知らなくてもディープラーニングを扱うことはできますが、ディープラーニングの学習に関する基本事項なので、是非この機会に理解するようにしてみて下さい!
本格的にAIを学ぶならキカガク長期コース
本記事では、基礎的な内容について解説を行ないましたが、より本格的にAIを学んでみたいという方にはキカガク長期コースの受講をお薦めします。
- 基礎理論からAI搭載のWEBアプリ開発まで幅広く学習可能
- 将来追加されるものも含めて、プロによる全ての講義動画がずっと見放題
- 質問し放題のチャットや定期的な個別メンタリングなどのサポート体制
- IT専門のキャリアアドバイザーによる転職サポート
- 中央省庁からの給付金対象であるため受講料が最大70%
- ディープラーニングE資格の受験資格を獲得可能
興味はあるけど、いきなり受講を申し込むには抵抗があるという方は、キカガク長期コースの無料オンライン説明会も是非活用してみてください!!













