今回のテーマは画像認識モデルのResNetです。
ResNetは、2014年のILSVRCの優勝モデルであるGoogleNet(22層)を遥かに上回る152層の構造を擁して、2015年のILSVRCで優勝したモデルです。画像の誤認識率で見ても、前年のGoogleNetの7%から3.5%へと大きく改善しています。
GoogleNetでも十分すごいモデルだと言われていたにも関わらず、それを上回るResNetがどんな工夫をして性能を伸ばしたのかを分かりやすく説明していきたいと思います。
モデルの多層化の壁
一般的にCNNのモデルは多層になればなるほど、その性能が向上すると考えられていました。
現にGoogleNet(22層)はVGG(16層)よりもILSVRCにおいて好成績を残していますから、この考えはある程度正しいと考えられます。
しかし、実際には話はそう単純ではありませんでした。確かに多層化をすればモデルの表現力は上がりそうですが、その一方で勾配消失問題に直面します。
勾配消失問題とは、ニューラルネットワークの層が深くなることによって、学習時に誤差が伝搬されず、結果的に勾配がほぼゼロとなってしまう現象です。
勾配がほぼゼロになると、ニューラルネットワークの学習が進まなくなるので、画像認識において、当然良い結果を出せるはずはありません。
GoogleNetを超える多層モデルを構築しようと考えた時に、まさにこのような層を増やしたいけど増やせないという壁が立ちはだかっていました。
この壁を突破したのがこれらから説明するResNetです。
ResNetは果たしてどのような手法によって、この壁を突破したのでしょうか?
ResNetの特徴
結論から言ってしまうと、ResNetではスキップ接続(skip connection)という手法を用いて、モデルの多層化の壁を突破しました。これがResNetの最大の特徴です。
というわけで、まずスキップ接続がどのようなものかを確認していきましょう。こちらがスキップ接続を模式的に表した図です。
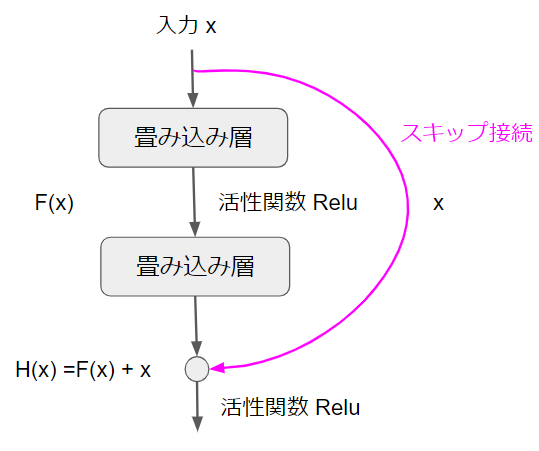
初めに入力値$x$があります。簡単のために、$x$と書いていますが、畳み込み層への入力値なので、これまでどおり画像データのことだと考えていただいた結構です。
そして、入力$x$が畳み込み層の方向とスキップ接続の方向の2つに分岐していることが分かると思います。先に馴染みのある畳み込み層の方向を確認しておきましょう。
畳み込み層の方は通常のCNNと何ら変わりはありません。畳み込みを経て活性化関数が適応されるという流れです。ここでは、畳み込み層を2つくぐった後の出力を$F(x)$という記号で表現しています。
一方、スキップ接続の方は、名前の通り、畳み込み層をスキップして、何もないまま一気に出力まで飛んでいます。入力の値がそのまま出力に加算されることになります。
結果として、このブロックの出力は$F(x) + x$となります。繰り返しになりますが、通常のCNNであれば出力は$F(x)$のみですが、スキップ接続によって、入力がそのまま出力に飛んでくるため、$F(x) + x$になるということです。
なぜ勾配消失問題を回避できるのか?
ResNetの最たる特徴であるスキップ接続の構造は、ここまでで説明したとおりですが、この構造でなぜモデルの多層化の壁を突破できるのかが分かりませんね。
モデルの多層化の壁とは、言い換えれば勾配消失問題なので、スキップ接続がどうやって勾配消失問題を回避するのかを見ていきましょう。
先ほどのスキップ接続の図に誤差逆伝搬(オレンジ)を追記しました。
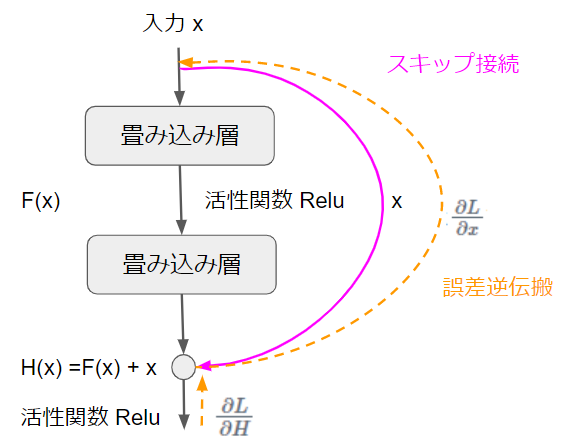
まず、このブロックまで伝わってきた誤差を$\frac{\partial L}{\partial H}$とします。$L$は損失関数です。スキップ接続で伝搬される誤差は$\frac{\partial L}{\partial x}$です。
では、ここで以下に示す微分の連鎖率を使って、$\frac{\partial L}{\partial x}$を計算してみましょう。
$\frac{\partial E}{\partial X} = \frac{\partial E}{\partial Y} \frac{\partial Y}{\partial X}$
$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial H} \frac{\partial H}{\partial x}$
先ほども言いましたが、$\frac{\partial L}{\partial H}$は伝搬してきた誤差です。では、$\frac{\partial H}{\partial x}$の方はどうでしょうか?
$\frac{\partial H}{\partial x} = \frac{\partial (F(x)+x)}{\partial x}= \frac{\partial F}{\partial x} +1$
では、ここで得られた$\frac{\partial H}{\partial x}$を$\frac{\partial L}{\partial x}$の数式に代入してみます。
$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial H} (\frac{\partial F}{\partial x} +1) = \frac{\partial L}{\partial H}\frac{\partial F}{\partial x} + \frac{\partial L}{\partial H}$
ここで注目してもらいたいのは一番右の数式の第2項です。くどいですが、$\frac{\partial L}{\partial H}$は伝搬してきた誤差です。その誤差が減衰することなくそのまま伝わっていることがこの数式から分かります。
ちなみに、第1項については、$\frac{\partial L}{\partial H}$に$\frac{\partial F}{\partial x}$が掛け算されているので、誤差が減衰している可能性があります。
勾配消失問題は、誤差がたくさんの層を伝搬していく間に、ほぼゼロになってしまうことが原因なので、減衰しないでそのまま誤差を伝えていくことができれば回避することができます。
これがスキップ接続によって勾配消失問題を回避できる理由です。
ResNetの構造
では、ResNetの構造を確認しておきましょう。こちらがResNetの全体像です。
Deep Residual Learning for Image Recognition
細かいところは見づらいかもしれませんが、左側が入力、右側が出力です。図の上方に飛び出している曲線がスキップコネクションです。
スキップ接続を含むブロックのことを残差ブロック(Residual Block)と言います。
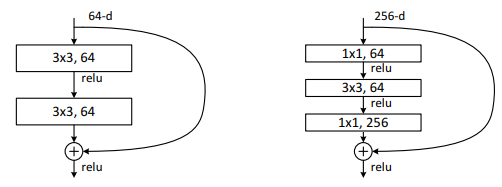
以下の図に示すように、ResNetには2種類の残差ブロックがあり、それぞれPlainアーキテクチャ(左)とBottleneckアーキテクチャ(右)と呼ばれています。
Deep Residual Learning for Image Recognition
2つのアーキテクチャのパラメーター数を計算してみると以下のようになります。
Plain:$(64×3×3×64) + (64×3×3×64) = 73,728$
Bottleneck:$(256×1×1×64) + (64×3×3×64)+(64×1×1×256)=69,632$
つまり、Bottleneckアーキテクチャの方がパラメーター数を抑えながら多層化を実現できているということになります。
そういう背景があり、152層のResNetではBottleneckアーキテクチャが採用されています。
補足:ResNetの幅を広げたWideResNet
ここまで、スキップ接続を導入して多層化に成功したのがResNetだと説明してきました。
もちろん、それは間違いではないのですが、「層を深くするのが本当に正解なのか?」という観点でResNetを見直したのがWideResNetです。
WideResNetでは、層を追加してCNNをどんどん深くしていく代わりに、各層の幅を広くしようというのが基本的な発想です。
「幅を広くする」というのは具体的に言えば、各層のチャネル数を増やすことです。
論文では、152層のResNetよりも、チャネル数2倍の50層のResNet(=WideResNet)の方が画像認識の性能がよいことが報告されています。
ResNetの説明は以上です!
ResNetのすごさが少しでも伝わったのであれば幸いです!
本格的にAIを学ぶならキカガク長期コース
本記事では、基礎的な内容について解説を行ないましたが、より本格的にAIを学んでみたいという方にはキカガク長期コースの受講をお薦めします。
- 基礎理論からAI搭載のWEBアプリ開発まで幅広く学習可能
- 将来追加されるものも含めて、プロによる全ての講義動画がずっと見放題
- 質問し放題のチャットや定期的な個別メンタリングなどのサポート体制
- IT専門のキャリアアドバイザーによる転職サポート
- 中央省庁からの給付金対象であるため受講料が最大70%
- ディープラーニングE資格の受験資格を獲得可能
興味はあるけど、いきなり受講を申し込むには抵抗があるという方は、キカガク長期コースの無料オンライン説明会も是非活用してみてください!!